Circumference Calculator
Circumference Calculation Explained
Understanding what a circumference of a circle is and how to calculate it is crucial as you move to higher level math. In this article you will learn the answers to the following questions.
- What is the circumference of a circle?
- How can you calculate the circumference of a circle?
What is the circumference of a circle?
The circumference of a circle is the distance around the outside of the circle. It is like the perimeter of other shapes like squares. You can think of it as the line that defines the shape. For shapes made of straight edges this line is called the perimeter but for circles this defining line is called the circumference.
This diagram shows the circumference of a circle.

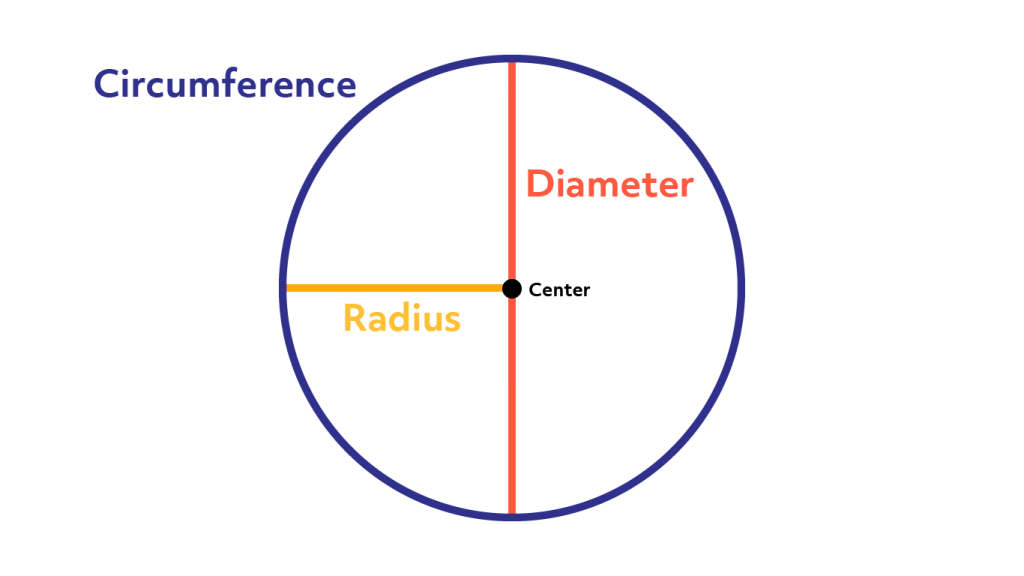
There are two other important distances on a circle, the radius (r) and the diameter (d). The radius, the diameter, and the circumference are the three defining aspects of every circle. Given the radius or diameter and pi you can calculate the circumference. The diameter is the distance from one side of the circle to the other at its widest points. The diameter will always pass through the center of the circle. The radius is half of this distance. You can also think of the radius as the distance between the center of the circle and its edge.
This diagram shows the circumference, diameter, center, and radius on a circle.
How can you calculate the circumference of a circle?
If you know the diameter or radius of a circle, you can work out the circumference. To begin with, remember that pi is an irrational number written with the symbol π. π is roughly equal to 3.14.
The formula for working out the circumference of a circle is:
Circumference of circle = π x Diameter of circle
This is typically written as C = πd. This tells us that the circumference of the circle is three “and a bit” times as long as the diameter. We can see this on the graphic below:

You can also work out the circumference of a circle if you know its radius. Remember that the diameter is double the length of the radius. We already know that C = πd. If r is the radius of the circle, then d = 2r. So, C = 2πr.
Example 1
If a circle has a diameter of 10cm, what is its circumference?
Answer
We know that C = πd. Since the diameter is 10cm, we know that C = π x 10cm = 31.42cm (to 2 decimal places).
Example 2
If a circle has a radius of 3m, what is its circumference?
Answer
We know that C = 2πr. Since the radius is 3m, we know that C = π x 6m = C= 18.84m (to 2 decimal places).
Example 3
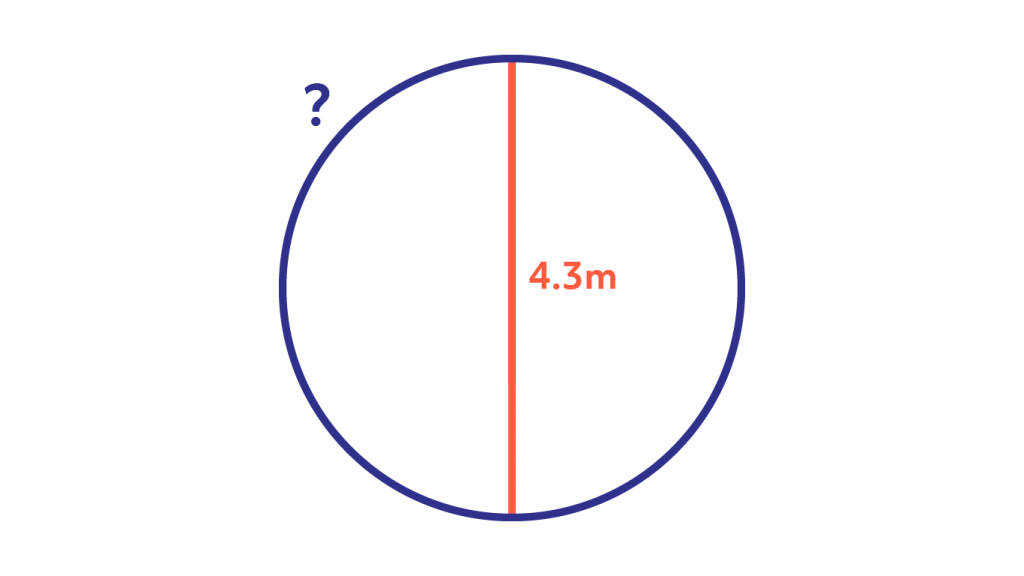
Find the missing length (marked with a ?) on the diagram below:
Answer
The missing length is the circumference. Using the knowledge that the diameter is 4.3m on the diagram and knowing that C = πd, we can calculate the circumference. With a little thinking we can easily figure out that, C = π x 4.3m = 13.51m (to 2 decimal places). The missing length is 13.51m.
How to calculate the circumference of the Earth
Have you ever wondered how big the earth is? Well, using pi it’s possible to work out the circumference of the Earth! Scientists have discovered that the diameter of the Earth is 12,742km. Given this information, what is the circumference of the Earth? Get out a piece of paper and a calculator and see if you can work it out on your own.
Again, we know that C = πd, and that the diameter of the earth is 12,742km. Using this information we can calculate the circumference of the Earth as C = π x 12,742km = 40,030km.
Formula for the Circumference and Area of a Circle
@mometrixNeed a circumference calculator? Click the link in our bio! ##pi ##piday ##circumference ##math ##mathematics ##mometrix


