How to Add Fractions
This guide shows you how to combine fractions with addition and subtraction. We have also included fractions with different denominators, which require a bit more work.
First, let’s start with a “how to” video on adding and subtracting fractions:
Fractions are nothing more than a ratio of a “part” to a “whole.” Fractions can be added, subtracted, multiplied and divided by understanding the structure of a fraction and by following a few simple rules. This article will show you how, but first let’s review the basics of fraction terminology.
Imagine one side of a magic cube, as shown below. It is divided into small squares of different colors that are all the same size. What is the fraction of yellow squares?

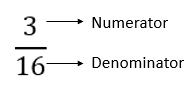
To determine this fraction, we need to count the yellow squares and relate that value to the total number of squares. The “part”, in this case, is the three yellow squares, which is known as the numerator of the fraction. This value is divided by the total number of squares, or the “whole”. There are sixteen squares in all, and this value is the denominator of the fraction.
When writing a fraction, division is typically notated with a horizontal line, with the numerator written above and the denominator written below.
Now let’s try writing another fraction:

What is the fraction of red squares?
Yes, that’s right! It is \(\frac{4}{16}\). However, this fraction can be simplified and written as: \(\frac{1}{4}\).
Please take a minute to review our detailed article on how to simplify fractions to review this concept if needed!
Now, if you are asked what is the fraction of red and yellow squares combined, how would you answer? It is as simple as it sounds: simply count the total number of red and yellow squares to get the numerator. The denominator stays the same:
Total red and yellow squares: 3 + 4 = 7
Fraction of combined red and yellow squares: \(\frac{7}{16}\)
This means that if the fraction of yellow squares is added to the fraction of red squares the answer must be \(\frac{7}{16}\).
Before we work through another problem, here’s a list of helpful things to remember:
- When adding and subtracting fractions, the denominators do not change. The addition or subtraction is performed only with the numerators.
- Before you can add or subtract a fraction, the denominators of your fractions must be the same as each other.
- Always try to simplify fractions before operating with them to keep the numbers that you are working with as small as possible.
Using these squares helps in visualizing the concept of adding fractions, but remember that most of the time visual figures are not available. So, let’s take away the visuals and work through the mathematical steps with some examples:
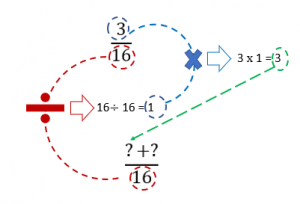
Suppose you don’t have the square available to consult and you are just asked to add \(\frac{3}{16}\) and \(\frac{1}{4}\). As you can see, the denominators of these fractions are not the same. This needs to be fixed before we can move on:
Step 1
Find LCM (Least Common Multiple) of the denominators of both fractions. Note that when working with fractions, the LCM is also referred to as the Least Common Denominator (LCD), because our goal is to match the denominators of the fractions.
We have a useful article on determining the GCF and LCM, which may be helpful for a review, but we will cover the steps here as well:
Mini-Step 1.1: List the prime factors of both numbers:
4 = 1 × 2 × 2
16 = 1 × 2 × 2 × 2 × 2
Mini-Step 1.2: Write the prime factors in index form.
Index form means that a repeating factor will be written as a factor raised to a power. For example, when 2 is multiplied four times it can be written as 2 raised to the 4th power: \(2^{4}\). When a number has no power indicated, it simply has a power of 1.
\(4 = 1\times 2^{2}\)
\(16 = 1\times 2^{4}\)
Mini-Step 1.3: Identify the common prime factors of each number.
To determine the LCD, the maximum power of common factors is used, along with any other prime factors that may exist between the two numbers.
\(1\times 2^{4}\)
Step 2
Multiply these factors and write the value as the denominator of the fraction.
\(1\times 2^{4}\) = 16
LCD = 16
Step 3
(Here comes the tricky part, pay attention!)
Once we know the LCD of each fraction, we need to make an adjustment to one or both of the original fractions. Let’s look at one fraction at a time and consider the following question: Does the denominator match the LCD?
The first fraction is \(\frac{3}{16}\), and the answer to the question is yes! The denominator of 16 equals the LCD of 16. This fraction does not need to be adjusted.
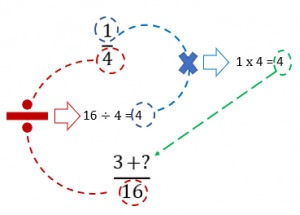
The second fraction is \(\frac{1}{4}\). Clearly, 4 is not equal to the LCD of 16. This fraction must be adjusted to create an equivalent fraction with a denominator of 16. But how?
The adjustment is simple: Determine the number that you have to multiply the denominator of 4 by to get the LCD. To do this, simply divide the LCD by the original denominator. In this case, \(16\div 4=4\).
Now the original fraction can be adjusted by multiplying both the numerator and denominator by this factor of 4, as shown:
\((\frac{4}{4}\times \frac{1}{4})=\frac{4\times 1}{4\times 4}=\frac{4}{16}\)
Remember that when multiplying fractions, perform the operation “straight across”, meaning (numerator x numerator) and (denominator x denominator).
This multiplication by \(\frac{4}{4}\) does not change the value of the original fraction because \(\frac{4}{4}\) = 1.
Once the equivalent fraction of \(\frac{4}{16}\) is determined, the fractions can be added:
\(\frac{3}{16}+\frac{4}{16}=\frac{3+4}{16}=\frac{7}{16}\)
As you can see, this is exactly what we got when we were adding the fractions of yellow and red squares!
These pictures may be helpful for those of you who prefer a visual demonstration of determining an LCD before adding or subtracting fractions:
Let’s do another example where one fraction is a proper fraction (numerator smaller than denominator) and the second one is an improper fraction (numerator is greater than denominator). The method of addition is the same and it does not matter whether the fraction is proper or improper.
Add: \(\frac{1}{12}+\frac{19}{18}\)
Try to do it yourself before going through the solution.
Step 1
Find LCM
Mini-Step 1.1:
12= 1 × 2 x 2 × 3
18 = 1 × 2 x 3 × 3
Mini-Step 1.2:
\(12 = 1\times 2^{2}\times 3\)
\(18 = 1\times 2\times 3^{2}\)
Mini-Step 1.3: Factors 1 and 2 and 3 occur for both numbers, and their maximum power is chosen, meaning that we will include (22) and (32) in our calculation:
\(1\times 2^{2}\times 3^{2}\)
Step 2
Multiply these factors and write the value as the denominator of the fraction.
\(1\times 2^{2}\times 3^{2} =36\)
LCD = 36
Step 3
Now it is time to figure out which fractions need to be adjusted to create like denominators. For each fraction ask, “does the denominator match the LCD?”
The first fraction is \(\frac{1}{12}\), and we can see that 12 does not equal the LCD of 36, so this fraction will have to be adjusted. As before, divide the LCD by the original denominator. In this case, \(36\div 12=3\).
Now the original fraction can be adjusted by multiplying both the numerator and denominator by 3, as shown:
\((\frac{3}{3}\times \frac{1}{12})=\frac{3\times 1}{3\times 12}=\frac{3}{36}\)
The second fraction, \(\frac{19}{18}\), must also be adjusted, as 18 does not match the LCD.
Divide the LCD by the denominator, 18: \(36\div 18=2\).
Multiply the numerator and denominator of the second fraction by 2, as shown:
\((\frac{2}{2}\times \frac{19}{18})=\frac{2\times 19}{2\times 18}=\frac{38}{36}\)
Now that each denominator matches the LCD, the equivalent fractions can be added:
\(\frac{3}{36}+\frac{38}{36}=\frac{3+38}{36}=\frac{41}{36}\)
Adding more than two fractions
At this point in the article, we hope that you have mastered the art of adding two fractions. If you have to add more than two fractions, the procedure is the same. Let’s do an example to illustrate it.
Add: \(\frac{4}{5}+\frac{1}{2}+\frac{1}{4}\)
These fractions are all in simplest form, so let’s start the process of finding the LCM and adjusting each fraction so the denominators are all the same.
Step 1
Find LCM
Mini-Step 1.1:
5 = 1 × 5
2 = 1 × 2
4 = 1 × 2 × 2
Mini-Step 1.2:
5 = 1 × 5
2 = 1 × 2
4 = 1 × \(2^{2}\)
Mini-Step 1.3: Choose highest powers of common factors for LCM and any additional factors of the three values:
1 × \(2^{2}\) × 5
Step 2
Multiply these factors and write the value as the denominator of the fraction
1 × \(2^{2}\) × 5 = 20
LCD = 20
Step 3
Now it is time to figure out which fractions need to be adjusted to create like denominators. For each fraction ask, “does the denominator match the LCD?”
The first fraction is \(\frac{4}{5}\), and we can see that 5 does not equal the LCD of 20. As before, divide the LCD by the original denominator. In this case, \(20\div 5=4\).
Now the original fraction can be adjusted by multiplying both the numerator and denominator by 4, as shown:
\((\frac{4}{4}\times \frac{4}{5})=\frac{4\times 4}{4\times 5}=\frac{16}{20}\)
The second fraction, \(\frac{1}{2}\), must also be adjusted, as 2 does not match the LCD.
Divide the LCD by the denominator, 2: \(20\div 2=10\)
Multiply the numerator and denominator of the second fraction by 10, as shown:
\((\frac{10}{10}\times \frac{1}{2})=\frac{10\times 1}{10\times 2}=\frac{10}{20}\)
Finally, determine the adjustment that needs to be made to the third fraction, \(\frac{1}{4}\).
Divide the LCD by the denominator, 4, for a factor of 5. Adjust the third fraction by multiplying by \(\frac{5}{5}\).
\((\frac{5}{5}\times \frac{1}{4})=\frac{5\times 1}{5\times 4}=\frac{5}{20}\)
Now that each of the three denominators match the LCD, the equivalent fractions can be added:
\(\frac{16}{20}+\frac{10}{20}+\frac{5}{20}=\frac{16+10+5}{20}=\frac{31}{20}\)
Adding fraction and integers
Another important concept to keep in mind while learning the addition of fractions is how to add fractions to integers. Fortunately, any integer can be rewritten to “look” like a fraction by dividing it by one. For example,
4 = \(\frac{4}{1}\)
30 = \(\frac{30}{1}\)
72 = \(\frac{72}{1}\)
Once the integer is written as a fraction over one, the process of adding and subtracting is the same as what we have discussed in this article.
Here are a few examples:
Add: 3 + \(\frac{3}{14}\)
This question can be rewritten as: \(\frac{3}{1}\) + \(\frac{5}{14}\)
Step 1
Determine the LCD with a little thought. What is the smallest number that both 14 and 1 can divide into evenly?
How about 14? This is the smallest number that both 1 and 14 can divide into evenly, Use this as the LCD to adjust the first “fraction”, \(\frac{3}{1}\).
Divide the LCD by the denominator of 1: \(14\div 1=14\)
Multiply the first fraction by \(\frac{14}{14}\).
\((\frac{14}{14}\times \frac{3}{1})=\frac{42}{14}\)
Since the denominators match, you are ready to add the fractions:
\(\frac{42}{14}+\frac{3}{14}=\frac{42+3}{14}=\frac{45}{14}\)
Final Thoughts!
In this article, we learned how to add fractions and how to add integers to fractions. This is a pretty useful skill to master and lays down the foundation of some advanced mathematical work. Want to have a shortcut? Try our fraction calculator! Check out the rest of our website for other interesting and useful mathematical concepts explained in an easy way. Need additional help, video reviews, or practice questions? Click here!


