How to Subtract Fractions
Mathematically, when we want to refer to only a part of something, we use fractions. For example, when someone says they drank half a glass of milk, mathematically they’re saying that they drank a fraction of the glass of milk (½ of the glass). Now, only one half of the glass is full of milk. This is a simple example of subtracting fractions, which is the topic of this article. Let’s look at another story to practice this important skill further.
Mike invited his friends over to play some board games. He ordered a pizza for the three of them to enjoy and each one of them took one of the eight slices.

Mike’s hungry little sister, Kim, walked by and pleaded with them to share the pizza with her! With 3 slices gone, only 5/8ths of the pizza was left and Mike told his little sister to take as much as she wanted.
She took 3 slices, or 3/8ths of the original pizza. What fraction of the pizza is left?
When you have a picture, it is pretty easy to see that there were two slices left. But we typically do not have such straightforward stories to work with. Before we dive into the mathematical procedure of subtracting fractions, let’s start with this “how-to” video.
For more help, refer to our articles on simplifying fractions and adding fractions, and, of course, always feel free to use our fraction calculator.
As you saw from the video, the concepts of adding and subtracting fractions are pretty much the same until the very last step. The two things to remember is that before adding or subtracting,
1) The denominators of the fractions must be the same, and
2) The adding and subtracting is done with only the numerators of the fractions.
Let’s look at our pizza example again with this in mind.
When the pizza was first delivered, there were eight slices to share, so the “whole” pizza can be represented by the fraction, \(\frac{8}{8}\). The boys and Kim ate six slices in total, or \(\frac{6}{8}\), of the pizza. Because both of these fractions have a denominator of 8, the subtraction can be done by simply subtracting the numerators, as shown:
\(\frac{8}{8}-\frac{6}{8}=\frac{8-6}{8}=\frac{2}{8}\), which can be simplified to \(\frac{1}{4}\)

Subtracting fractions with different denominators:
What if the fractions do not have the same denominator? Well, that will require some additional work. The Least Common Multiple (LCM) will have to be determined, and one or both of the fractions will have to be adjusted so their denominators “match” the LCM.
This may sound complicated, but after a few examples, it will all start to make more sense!
Example 1:
Simplify: \(\frac{7}{9}-\frac{3}{16}\)
The instructions to “simplify” are asking you to subtract the two fractions. You can see that the denominators are not the same, so let’s get to work on adjusting one or both fractions so their denominators “match”.
Step 1: Determine the LCM of the denominators, 9 and 16.
Mini-Step 1.1: List the prime factors of both numbers:
9 = 1 × 3 × 3
16 = 1 × 2 × 2 × 2 × 2
Mini-Step 1.2: Write the prime factors in index form.
This means that a repeating factor will be written as a factor raised to a power. For example, when 2 is multiplied four times it can be written as 2 raised to the 4th power, or \(2^{4}\).
Also note that when a number has no power indicated, it has a power of 1.
\(9 = 1\times 3^{2}\)\(16 = 1\times 2^{4}\)
Mini-Step 1.3: Choose the maximum power of common factors, and any other factors that may exist between the numbers.
\(1\times 3^{2}\times 2^{4}\)
Step 2: Multiply these factors for the LCM.
\(1\times 3^{2}\times 2^{4}=144\)
LCM = 144
Step 3: Adjust the fractions, if necessary.
Once we know the LCM, we need to make an adjustment to one or both of the original fractions if their denominators do not equal that value. Simply ask the question, “Does the denominator match the LCM?”
In this example, both fractions will need to be algebraically adjusted because their denominators of 9 and 16 do not match the LCM of 144.
The adjustment is simple: divide the LCM by the original denominator. In this case, \(144 \div 9 = 16\).
Now the original fraction can be adjusted by multiplying both the numerator and denominator by this factor of 16, as shown:
\((\frac{16}{16}\times \frac{7}{9})=\frac{16\times 7}{16\times 9}=\frac{112}{144}\)
Remember that when multiplying fractions, perform the operation “straight across”, meaning (numerator x numerator) and (denominator x denominator).
Note that this multiplication by \(\frac{16}{16}\) does not change the value of the original fraction because \(\frac{16}{16}\) = 1! The result is a fraction that is equivalent to the original.
Now let’s go through the same process for the second fraction, \(\frac{3}{16}\). Clearly, 16 does not equal the LCM of 144. The factor that we need to make the necessary adjustment is \(144\div 16 = 9\)
Adjust the second fraction as shown:
\((\frac{9}{9}\times \frac{3}{16})=\frac{9\times 3}{9\times 16}=\frac{27}{144}\)
The denominators of the equivalent fractions now match, so we are ready to subtract.
\(\frac{112}{144}-\frac{27}{144}=\frac{112-27}{144}=85\)
Subtracting more than two fractions
As is the case of addition, subtracting more than two fractions involves the same procedure.
Example 2:
Simplify: \(\frac{3}{4}-\frac{1}{3}-\frac{1}{10}\)
Step 1: Determine the LCM of the denominators, 4, 3 and 10.
Mini-Step 1.1: List the prime factors of each number.
4 = 1 × 2 × 2
3 = 1 × 3
10 = 1 × 2 × 5
Mini-Step 1.2: Write the prime factors in index form.
\(4 = 1\times 2^{2}\)\(3 = 1 \times 3\)
\(10 = 1\times 2\times 5\)
Mini-Step 1.3: Choose the highest powers of each factor for LCM.
**Remember: If a factor occurs in only one number it is always chosen.
\(1\times 2^{2}\times 3\times 5\)
Step 2: Multiply these factors for the LCM:
\(1\times 2^{2}\times 3\times 5 = 60\)
LCM = 60
Step 3: Adjust each fraction so the denominators match the LCM
Divide the LCM by the denominator of the first fraction: 60 ÷ 4 = 15. Adjust the first fraction, as shown:
\((\frac{15}{15}\times \frac{3}{4})=\frac{45}{60}\)
Repeat the procedure for the second fraction: 60 ÷ 3 = 20
\((\frac{20}{20}\times \frac{1}{3})=\frac{20}{60}\)
Finally, the third fraction needs to be adjusted by a factor of 60 ÷ 10 = 6.
\((\frac{6}{6}\times \frac{1}{10})=\frac{6}{60}\)
We are now ready to subtract the equivalent fractions: \(\frac{45-20-6}{60}=\frac{19}{60}\)
So, the final answer is \(\frac{19}{60}\).
Subtraction of fraction and integers
So far, we have learned all about subtracting fractions. However, there are times when you are required to find the difference of a fraction and an integer. This section will explain how to do that.
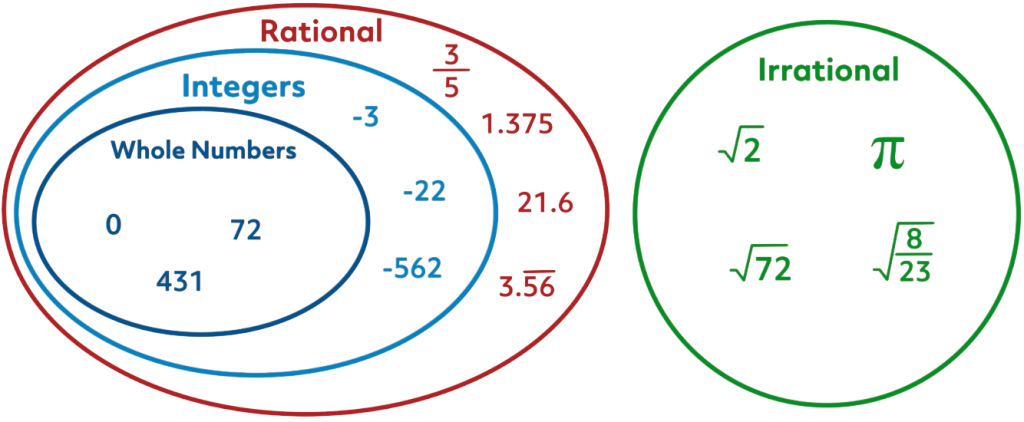
First let’s review the different classifications of the Real number system. This image shows that Integers, which are whole numbers, are a subset of Rational numbers. As the name suggests, Rational numbers are those that can be written as a “ratio”, which is just another word for fraction. This is important because it reveals that an integer can be written as a fraction with a denominator of 1.
Here are some examples of integers written as fractions:
8 = \(\frac{8}{1}\); 5 = \(\frac{5}{1}\); 20 = \(\frac{20}{1}\)
Using this information, you can now use the steps that we have covered to subtract fractions from integers.
Example 3:
Simplify: \(4 – \frac{7}{15}\)
This expression can be rewritten as: \(\frac{4}{1} – \frac{7}{15}\)
Step 1: Determine the LCM of the denominators, 1 and 15.
Mini-Step 1.1: Determine the prime factors of the denominators
1 = 1
15 = 1 × 3 × 5
Mini-Step 1.2: There are no factors with powers.
1 = 1
15 = 1 × 3 × 5
Mini-Step 1.3: Choose the factors of each denominator.
1 × 3 × 5
Step 2: Multiply these factors for the LCM.
1 × 3 × 5 = 15
LCM = 15
Step 3: Adjust fraction(s) so the denominators match the LCM
Divide the LCM by the denominator of the first fraction: 15 ÷ 1 = 15
Adjust the first fraction: \((\frac{15}{15}\times \frac{4}{1})=\frac{60}{15}\)
The second fraction, \(\frac{7}{15}\), does not need to be adjusted, so we are ready to subtract.
Finally, we have: \(\frac{60 – 7}{15}=\frac{53}{15}\)
Now you should have a full understanding of how to subtract fractions!

