Guide To Simplifying Fractions And Improper Fractions
This article will show you how to simplify fractions and improper fractions. We are sure that you are already familiar with the basics of fractions, but let’s have a brief review of them anyway to refresh your memory!
Also remember that our fraction calculator is always available for you to use.
Imagine that your mother made a delicious pie that is now going to be divided between you and your siblings.

If you have 3 siblings, the pie will be divided into 4 equal pieces, and you will each get one piece to eat. The fraction, \(\frac{1}{4}\), represents the “part” that you will eat divided by the total number of parts, or the “whole”. Obviously, if each of the four children eat their piece, then the whole pie will be gone!
To review, the correct terminology for the “part” of a fraction is the numerator, and the “whole” is called the denominator.

But what if your brother did not like the pie, and he gave his piece to you? You thought the pie was delicious, and ate it right up! What portion of the whole pie did you end up eating?
Well, you started with \(\frac{1}{4}\) and your brother gave you his portion of \(\frac{1}{4}\). Adding these together results in a fraction of \(\frac{1}{4}\)+\(\frac{1}{4}\)=\(\frac{1+1}{4}\), or \(\frac{2}{4}\). This image is helpful to illustrate just how much pie you ate:

By eating your brother’s piece of pie and your own, you actually ate one half of the pie. As you can see, the value of \(\frac{2}{4}\) is the same as the value of \(\frac{1}{2}\). In math, these fractions are referred to as equivalent fractions. The denominators are different, which means that the “whole” was divided into a different number of equal “parts”.
Suppose the pie was cut into six equal pieces. How many pieces would you have to eat for half of the pie to be gone?
Well, half of the six pieces is three, so the fraction, \(\frac{3}{6}\), is equivalent to \(\frac{1}{2}\).
This brings us to the topic of this article of simplifying fractions. As you have seen, fractions can represent the same amount, but look different, depending on how many “parts” are in the “whole”.
The process of simplifying fractions means to reduce the numerator and the denominator by their greatest common factor, or their GCF. In the example above, the numerator and denominator of the fraction, \(\frac{3}{6}\), share the GCF of 3. Dividing both numbers by the GCF of 3 results in :
\(\frac{3\div 3}{6\div 3}\)=\(\frac{1}{2}\)
If you need a refresher in how to find the GCF, check out our article on Finding GCF and LCM. Simplifying fractions in this way makes our work with more complex problems easier.
Now that you have a visual reference for fractions, let’s move on to some practice to familiarize yourself with the terminology and the step-by-step process of simplifying fractions:

Example 1:
The fraction, \(\frac{5}{25}\), has a numerator of 5 and a denominator of 25.
Step 1
Write the prime factors of both the numerator and the denominator:
5 = 1 × 5
25 = 1 × 5 × 5
Step 2
Identify the factors that are in both numbers, these are called common factors.
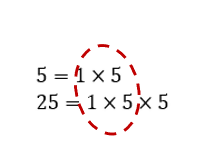
Step 3
Multiply the common factors identified in Step 2.
This result is referred to as the greatest common factor, or GCF: 1 × 5 = 5
Step 4
Divide both the numerator and denominator by the GCF to get the simplified fraction:\(\frac{5\div 5}{25\div 5}=\frac{1}{5}\)
Because \(\frac{5}{25}\) simplifies to \(\frac{1}{5}\), they are equivalent fractions.
Example 2:
The fraction, \(\frac{12}{18}\), has a numerator of 12 and a denominator of 18.
Step 1
Write the prime factors of both numerator and denominator:
12 = 1 × 2 × 2 × 3
18 = 1 × 2 × 3 × 3
Step 2
Identify the common factors:
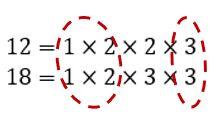
Step 3
Multiply the common factors identified in Step 2 for the GCF:
1 × 2 x 3 = 6
Step 4
Divide both the numerator and denominator by the GCF to get the simplified fraction: \(\frac{12\div 6}{18\div 6}=\frac{2}{3}\)
Because \(\frac{12}{18}\) simplifies to \(\frac{2}{3}\), they are equivalent fractions.
Example 3:
The fraction, \(\frac{12}{53}\) has a numerator of 12 and denominator of 51.
Step 1
Write the prime factors of both the numerator and denominator:
12 = 1 x 2 x 2 x 3
53 = 1 x 53
As you can see, these numbers only share a factor of 1. This is an example of a fraction that cannot be simplified because there are no common factors other than 1.
This type of fraction is said to be in simplest form.
Notice that in all of the examples we have looked at so far, the numerator is smaller than the denominator. This type of fraction is called a proper fraction. As you can imagine, the structure of an improper fraction is different, in that the numerator is greater than the denominator.
Fortunately, the steps of simplifying proper fractions also apply to simplifying improper fractions. There is some extra work, however, if you are asked to rewrite the simplified improper fraction into a mixed number. We’ll get into mixed numbers a little later.
Let’s do a few more examples.
Example 4:
Simplify the improper fraction, \(\frac{24}{9}\).
Follow steps 1 through 4 as explained above:
Step 1
Write the prime factors of both the numerator and the denominator:
24 = 1 × 2 × 2 × 2 × 3
9 = 1 × 3 × 3
Step 2
Identify the common factors:
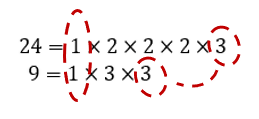
Step 3
Multiply the common factors identified in Step 2 for the GCF:
1 × 3 = 3
Step 4
Divide both the numerator and denominator by the GCF to get the simplified fraction:\(\frac{24\div 3}{9\div 3}=\frac{8}{3}\)
Because the fraction, \(\frac{24}{9}\), simplifies to \(\frac{8}{3}\), they are equivalent fractions.
Note: Simplifying an improper fraction will always result in an improper fraction.
As mentioned previously, students are sometimes required to convert an improper fraction to a mixed number, which is simply a representation with a whole number and a fraction.
Essentially, the denominator is divided by the numerator for the whole number, and the fraction represents the remainder written as a fraction of the denominator.
Step 5
Convert the fraction, \(\frac{8}{3}\), into a mixed number.
Divide the numerator by the denominator.
In this example, the numerator, 8, is the dividend and the denominator, 3, is the divisor:
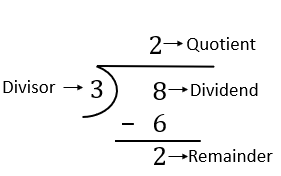
The quotient of a division problem is the answer to the question, “how many times does 3 divide into 8?”
Because 3 divides into 8 two times with 2 left over, which is known as the remainder, the mixed numeral representation is: \(2\frac{2}{3}\).
The fractional part of a mixed numeral will always be a proper fraction, because it represents a “part” of the next “whole.”
Now let’s put it all together with a final example.
Example 5:
Simplify the improper fraction,\(\frac{28}{12}\).
Step 1
Write the prime factors of both the numerator and the denominator:
28 = 1 × 2 × 2 × 7
12 = 1 × 2 × 2 × 3
Step 2
Identify the common factors:
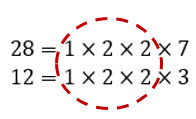
Step 3
Multiply the common factors identified in Step 2 for the GCF:
1 × 2 × 2 = 4
Step 4
Divide both the numerator and denominator by the GCF to get the simplified fraction:\(\frac{28\div 4}{12\div 4}=\frac{7}{3}\)
Step 5
Convert the fraction, \(\frac{7}{3}\), into a mixed number.
Divide the numerator by the denominator, as shown:
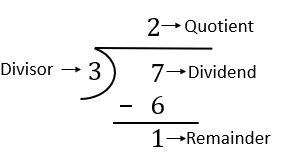
Write the result as a mixed numeral: \(2\frac{1}{3}\).
Something to think about:
Suppose you have the mixed number, \(4\frac{3}{9}\).
Given what you know about equivalent fractions, what needs to be done to simplify this mixed numeral?
Only the fraction would have to be simplified!
Because the greatest common factor of 3 and 9 is 3, divide both the numerator and denominator of the fraction by 3, resulting in \(\frac{1}{3}\). The fractions, \(\frac{3}{9}\) and \(\frac{1}{3}\), are equivalent, so the simplified mixed number is \(4\frac{1}{3}\).
Final Thoughts!
This article reviewed how to simplify fractions, both proper and improper, and we extended the concept to simplify mixed numbers. As mentioned, simplifying fractions before using them in computations make your work much easier to manage.
Check out our website for additional articles about fractions and related operations.
Need additional help, video reviews, or practice questions? Click here!

