Multiplying and Dividing Fractions

This article covers how to multiply and divide fractions.

First, let’s start with a quick “how to” video on multiplying fractions:

Multiplying Fractions

Now that you’ve seen the operations in action, we’ll explore why they work the way they do. Let’s revisit the connection between multiplication and division.

The equation $12\div 3 = 4$ can be visualized in two different ways:

If 12 is the whole and 3 is the number of equal groups, then 4 is the number in each group. This shows that $4\times 3 = 12$.

A diagram showing how 12 can be broken down into three sections of four

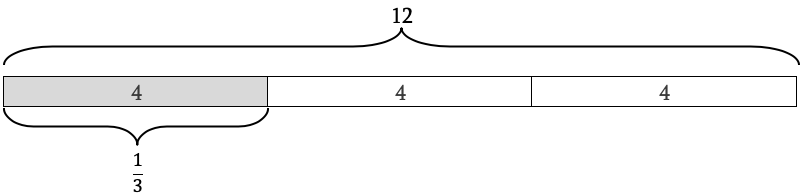
Notice this also shows that 4 is one third of 12.

If 12 is the whole and 3 is the number in each group, then 4 is the number of equal groups. This shows that $3\times 4 = 12$.

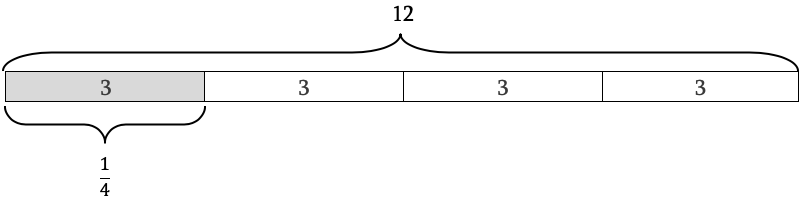
Here, it’s also true that 3 is one fourth of 12.

The word “of” is important here, as it simply means multiplication:

“$\frac{1}{3}$of 12 equals 4” means $12\times \frac{1}{3} = 4$. This is illustrated in one section of our diagram:

“$\frac{1}{4}$ of 12 equals 3” means $12\times \frac{1}{4} = 3$. Again, this is shown in our diagram:

Using either diagram above, what is $\frac{2}{3}$ of 12?

Since $\frac{1}{3}$ of 12 is 4, $\frac{2}{3}$ of 12 must be 4 + 4 = 8.

Suppose a 12-egg carton is $\frac{5}{6}$ full. How many eggs are in the carton?

We need to find $\frac{5}{6}$ of 12. In other words, what’s $12\times \frac{5}{6}$? Use a diagram to figure out how many eggs equals $\frac{1}{6}$ of 12.

Since $\frac{1}{6}$ of 12 is 2, $\frac{5}{6}$ of 12 is $2\times 5 = 10$. 10 eggs are in the carton.

This provides the basis for what you watched in the video about how to multiply fractions.

$How to multiply two fractions$

Using our examples (remember, any number can be expressed as a fraction with a denominator of 1):

$12\times \frac{1}{3} = \frac{12}{1}\times \frac{1}{3}=\frac{12\times 1}{1\times 3}=\frac{12}{3}=4$

$12\times \frac{1}{4} = \frac{12}{1}\times \frac{1}{4}=\frac{12\times 1}{1\times 4}=\frac{12}{4}=3$

$12\times \frac{2}{3} = \frac{12}{1}\times \frac{2}{3}=\frac{12\times 2}{1\times 3}=\frac{24}{3}=8$

$12\times \frac{5}{6} = \frac{12}{1}\times \frac{5}{6}=\frac{12\times 5}{1\times 6}=\frac{60}{6}=10$

Try these problems!

The baseball team played 16 games and won three fourths of them. How many games did they win?

Answer: 12 games.

$\frac{1}{4}$of 16 is 4, so $\frac{3}{4}$ of 16 is $3\times 4 = 12$.

Or you could solve it this way:

$\frac{16}{1}\times \frac{3}{4}=\frac{16\times 3}{4}=\frac{48}{4}=12$

What is $\frac{3}{5}$of 11?

Answer: $\frac{33}{5}$ or $6\frac{3}{5}$

A diagram is still helpful, even though 11 is not a multiple of 5.

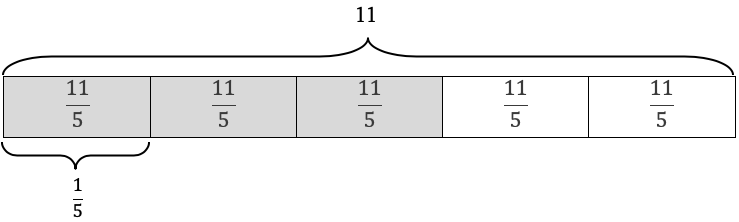
$\frac{1}{5}$ of 11 is $\frac{11}{5}$, so $\frac{3}{5}$ of 11 is $\frac{33}{5}$. $\frac{11}{1}\times \frac{3}{5}=\frac{11\times 3}{1\times 5}=\frac{33}{5}$.

Suppose you fold a sheet of paper into 3 equal rows and 4 equal columns, creating sections as shown below. What fraction of the area of the sheet of paper is each section?

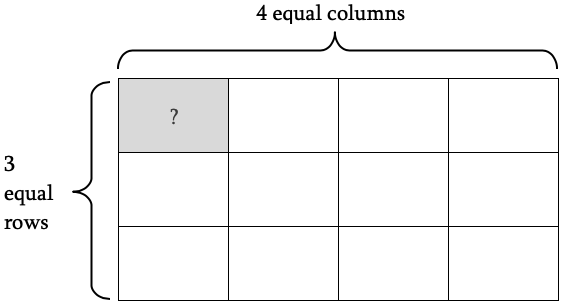
Since you divide the piece of paper into 4 equal columns, each column is one fourth of the total area of the piece of paper:

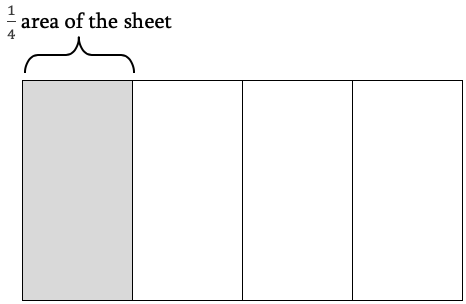
Dividing into thirds divides the sheet into 3 equal parts, but notice it also divides each column into 3 equal parts.

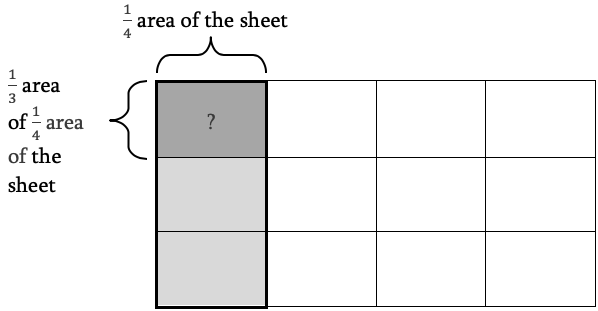
To find the size of one section, we need to figure out what fraction of the whole the section is.

By counting, one section equals $\frac{1}{12}$ of the whole, since each section is the same size.

Notice that each section is $\frac{1}{3}$ of a column. Since we know a column is $\frac{1}{4}$ of a sheet, we are calculating “one third of one fourth”. In other words, we multiply $\frac{1}{3}\times \frac{1}{4}=\frac{1\times 1}{3\times 4}=\frac{1}{12}$.

Let’s visualize the examples from the video. The first example presented was $\frac{2}{3}\times \frac{2}{5}$. The question we ask ourselves is: “What is $\frac{2}{3}$ of $\frac{2}{5}$ of a quantity?”

Here’s our whole.

Start by dividing into fifths and highlighting $\frac{2}{5}$:

Now, divide the whole by 3 in the horizontal direction and highlight 2 of those sections:

Each section represents $\frac{1}{15}$ of the whole, so four sections represent $\frac{4}{15}$ of the whole. Using multiplication, we can find $\frac{2}{3}$ of $\frac{2}{5}$ by $\frac{2}{3}\times \frac{2}{5}=\frac{2\times 2}{3\times 5}=\frac{4}{15}$.

$\frac{4}{7}\times \frac{3}{11}=\frac{4\times 3}{7\times 11}=\frac{12}{77}$, as seen in the clip.

Using a diagram, we can verify the result. Start by dividing a whole into sevenths by creating seven columns. Then divide the whole into elevenths by creating 11 rows. The intersection of 4 columns and 3 rows in this case gives us $\frac{12}{77}$ of the whole.

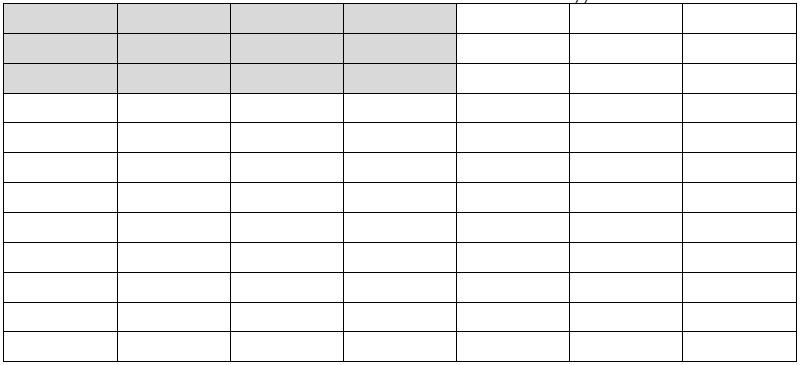
Practice time!

What is $\frac{5}{8}\times \frac{3}{4}$?

Answer: $\frac{15}{32}$

$\frac{5}{8}\times \frac{3}{7}=\frac{5\times 3}{8\times 4}=\frac{15}{32}$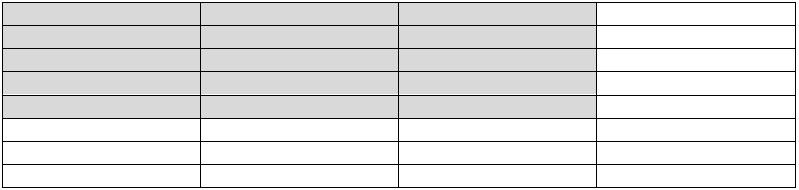

In your closet, $\frac{7}{12}$ of your pieces of clothing are tops and $\frac{3}{8}$ of those are t-shirts. What fraction of your clothes are t-shirts?

Answer: $\frac{7}{12}\times \frac{3}{8}=\frac{7\times 3}{12\times 8}=\frac{21}{96}=\frac{7}{32}$

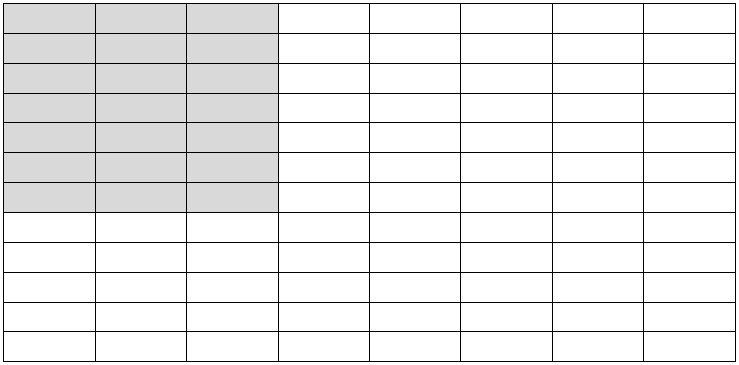
Multiplying mixed numbers works in the exact same way, except you’ll need to convert those to improper fractions in order to visualize the multiplication. Let’s see how it works!

$1\frac{1}{4}\times \frac{2}{3}$ can be written $\frac{5}{4}\times \frac{2}{3}=\frac{10}{12}=\frac{5}{6}$

Since $1\frac{1}{4}$ is more than 1, we start with 2 wholes instead of 1:

Next, divide both wholes into fourths and highlight 5 columns to represent $\frac{5}{4}$:

Then divide both wholes by 3 and highlight 2 rows to represent $\frac{2}{3}$:

The difference here is that each section is $\frac{1}{12}$ instead of $\frac{1}{24}$, because there are 2 wholes. In other words, each section is $\frac{1}{12}$ of one whole. Ten of those makes $\frac{10}{12}$.

Try $1\frac{2}{3}\times 2\frac{3}{5}$.

Answer: $\frac{5}{3}\times \frac{13}{5}=\frac{5\times 13}{3\times 5}=\frac{65}{15}=\frac{13}{3}$

To visualize, we’ll need 2 wholes to represent $1\frac{2}{3}$ and 3 to represent $2\frac{3}{5}$, for a total of 6 wholes.

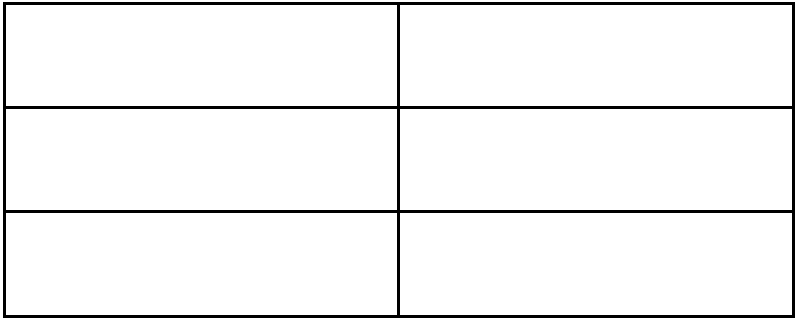
Divide the wholes into 3 columns each and highlight 5 to represent $1\frac{2}{3}$:

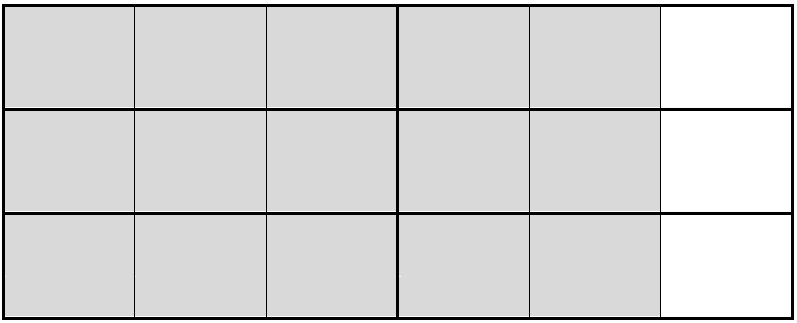
Then divide them into 5 rows each and highlight 13 to represent $\frac{13}{5}$:

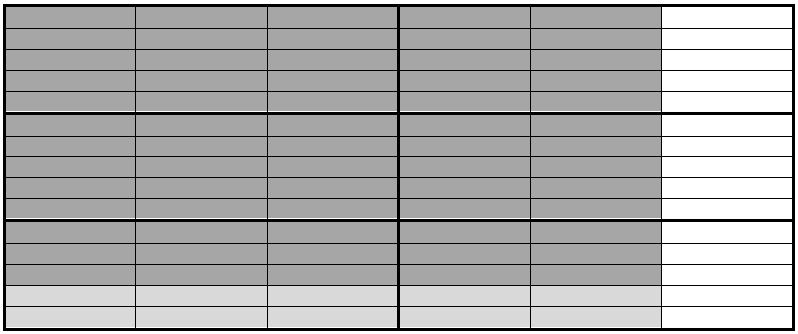
Remember, each section represents $\frac{1}{15}$ of one whole, not $\frac{1}{90}$ of all of the wholes combined. There are $\frac{65}{15}$ highlighted, or $\frac{13}{5}$.

Dividing Fractions

Let’s begin by revisiting the examples from the video.

First, $\frac{4}{5}\div 2$ was explored. We can translate this in various ways:

“What is one half of $\frac{4}{5}$?” Since dividing a number by 2 is the same as multiplying it by $\frac{1}{2}$, this makes sense.
“How many times does 2 go into $\frac{4}{5}$?”

Let’s look at a diagram, then we’ll revisit the method. Here’s $\frac{4}{5}$:

Half of $\frac{4}{5}$ is $\frac{2}{5}$:

So, $\frac{4}{5}\div 2=\frac{4}{5}\times \frac{1}{2}=\frac{4}{10}=\frac{2}{5}$

Similarly, here’s $\frac{4}{5}$ again:

Divide horizontally as we did with multiplication to get $\frac{4}{10}$:

Thinking about the relationship between multiplication and division, our result makes sense. $\frac{4}{5}\div 2$ means 2 times some number equals $\frac{4}{5}$. $2\times \frac{2}{5}=\frac{4}{5}$. Check!

In the video, you saw $\frac{2}{5}\div 3=\frac{2}{15}$. Let’s make sure we understand why:

Here’s $\frac{2}{5}$:

Divide $\frac{2}{5}$ by 3 because we are looking for $\frac{1}{3}$ of $\frac{2}{5}$:

We can see the solution of $\frac{2}{15}$

Understanding the relationship between multiplication and division leads to the commonly taught method called Keep-Change-Flip.

$Diagram showing how to divide fractions$

The last problem in the video explored $\frac{3}{5}\div \frac{7}{5}$. As it showed, $\frac{3}{5}\div \frac{7}{5}=\frac{3}{5}\times \frac{5}{7}=\frac{15}{35}=\frac{3}{7}$.

Time for a diagram!

Here’s $\frac{3}{5}$:

And here’s $\frac{7}{5}$:

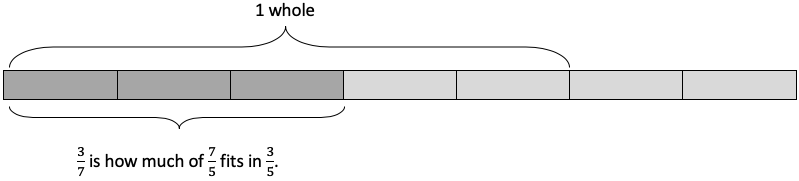
Multiplication and division are so similar because they are directly related to each other! What is the difference in these two sentences?

You have $\frac{3}{4}$ of a leftover pizza that you want to split between 6 friends. How much of the pizza does each person get?
You have $\frac{3}{4}$ of a leftover pizza, then you eat $\frac{5}{6}$ of that. How much of the pizza has been eaten?

Sentence 1 calls for division. You are dividing $\frac{3}{4}$ of a pizza into 6 equal parts: $\frac{3}{4}\div 6$ (which turns into multiplication anyway!).

$\frac{3}{4}\div 6=\frac{3}{4}\times \frac{1}{6}=\frac{3}{24}=\frac{1}{8}$

Each person gets one eighth (about a slice) of the original pizza.

Sentence 2 calls for multiplication. What is $\frac{5}{6}$ of $\frac{3}{4}$? $\frac{5}{6}\times \frac{3}{4}$.

$\frac{5}{6}\times \frac{3}{4}=\frac{5\times 3}{6\times 4}=\frac{15}{24}=\frac{5}{8}$

Five eighths have been eaten (or about 5 slices).

Final Thoughts!

When multiplying and dividing fractions, the procedures are important, but sometimes it can be difficult to interpret a situation and identify what is required. Translation into English sentences and modeling with diagrams can help you make sense of these fraction operations. Click for more help with fractions, decimals, and percentages. If you want to learn how to convert an improper fraction to a mixed number, see our article on Simplifying Fractions. Explore our resources further, to enhance your mathematical learning in an easy and fun way!