What is Pi?
~William L. Schaaf, Nature and History of Pi
Pi (often represented by the lower-case Greek letter π), one of the most well-known mathematical constants, is the ratio of a circle’s circumference to its diameter. For any circle, the distance around the edge is a little more than three times the distance across.
Typing π into a calculator and pressing ENTER will yield the result 3.141592654, not because this value is exact, but because a calculator’s display is often limited to 10 digits. Pi is actually an irrational number (a decimal with no end and no repeating pattern) that is most often approximated with the decimal 3.14 or the fraction \(\frac{22}{7}\).

This brings up a rather interesting question: If pi is the number of diameter lengths that fit around a circle, how can it have no end?
Pi: A Perennial Puzzle
Pi has interested people around the world for over 4,000 years. Many mathematicians – from famous ones such as Fibonacci, Newton, Leibniz, and Gauss, to lesser well-known mathematical minds – have toiled over pi, calculated its digits, and applied it in numerous areas of mathematics. Some spent the better parts of their lives calculating just a few digits. Here is a sampling of the many milestones in the life of pi.
Early decimal approximations for pi were obtained in a number of different ways. For example, in ancient Babylon, rope stretchers marking the locations of buildings and boundaries estimated pi to be \(\frac{25}{8}\) = 3.125. The ancient Egyptians determined the ratio to be \((\frac{16}{9})^{2}\) ≈ 3.16. The earliest calculations of pi were largely based on measurement.
Archimedes, a Greek mathematician, was the first to use an algorithmic approach to calculate pi. He drew a polygon inside a circle and drew a second polygon outside of the circle. Then he continuously added more and more sides of both polygons, getting closer and closer to the shape of the circle. Having reached 96-sided polygons, he proved that \(\frac{223}{71}\) < pi < \(\frac{22}{7}\).

From Archimedes’ time (about 250 B.C.E.) to the early 1600s mathematicians in countries around the world used methods similar to Archimedes’ to estimate pi, with increasingly efficient and accurate results. In 1630, Austrian astronomer Christoph Grienberger calculated 38 digits of pi using polygons with 1040 sides, which remains the best calculation of pi using this polygonal method.
The Renaissance saw many developments and work on pi, including the creation of the name pi. Until 1647, it didn’t have a universal name or symbol. English mathematician William Oughtred began calling it pi in his publication Clavis Mathematicae, but it wasn’t until Leonhard Euler used the symbol in 1737 that it became widely embraced. The reason for adopting this particular Greek letter is because it is the first letter of the Greek word, perimetros, which loosely translates to “circumference.”

In 1767, Swiss mathematician Johann Heinrich Lambert proved pi is irrational and in 1882 Ferdinand von Lindemann proved pi is transcendental, which means π cannot be a solution to a polynomial equation with rational coefficients. This finding is significant because, until this point, it was believed that one could construct a square and a circle with equal area, known as “squaring the circle”. Proving the transcendence of pi showed this is not possible and the phrase “squaring the circle” is now used as a metaphor for trying to do something that is impossible.
With modern technological advances, pi has now been calculated to 31 trillion digits. However, only the first 39 or so are needed to be able to perform all calculations in our observable universe with virtually no error. Though it is news every time the digit record is broken, we can now use technology to explore other aspects of pi. One example from the Chudnovsky brothers, a pair of American mathematicians:
“We are looking for the appearance of some rules that will distinguish the digits of pi from other numbers. If you see a Russian sentence that extends for a whole page, with hardly a comma, it is definitely Tolstoy. If someone gave you a million digits from somewhere in pi, could you tell it was from pi? We don’t really look for patterns; we look for rules”
Take some time to research and explore this unique number. It has a long and very detailed history that shows the field of mathematics as a living, breathing subject, not as a collection of rules and formulas.
@mometrixWanna know more about pi? Visit PiDay.org! Link in bio. ##piday ##pi ##pie ##math ##mathhelp ##mometrix♬ original sound – Mometrix Test Preparation
Where does pi occur?
Pi occurs in many areas of mathematics, far too many to list here.
The study of pi begins around middle school, when students learn about the circumference and area of circles.
CIRCUMFERENCE and AREA of CIRCLES
The definition of pi gives us a way to calculate circumference. The circumference of a circle is the distance around a circle. If π = \(\frac{C}{d}\), then C = πd. You can also calculate the circumference of a circle with C = 2πr.

The area of a circle is A = π\(r^{2}\).

This learning progresses as students study cylinders, spheres, and cones.
CYLINDERS, SPHERES, and CONES
The surface area of a cylinder is 2π\(r^{2}\) + h(2πr).

The volume of a cylinder is π\(r^{2}\)h.

The surface area of a sphere is 4π\(r^{2}\).

The volume of a sphere is \(\frac{4}{3}\)π\(r^{3}\).

The surface area of a cone is πrl + π\(r^{2}\).

The volume of a cone is \(\frac{1}{3}\)π\(r^{2}\)h.

In high school, students study circles more in-depth and also study unit-circle trigonometry.
RADIANS and DEGREES
Angles can be measured in both degrees and radians. A radian is defined as an arc that has the same measure as the radius of a circle. Since π diameters equal circumference, 2π radius lengths also equals circumference. Therefore, 360 degrees is the same as 2π radians, 180 degrees equals π radians, 90 degrees equals \(\frac{\pi}{2}\) radians, etc.

ARCS
An arc created by a central angle, θ, is a fraction of the circumference of a circle: arc length = \(\theta \frac{C}{2\pi}\). The equation for circumference can be substituted in, then the whole equation can be simplified to: arc length = \(\theta \frac{\pi d}{2\pi}=\theta \frac{d}{2}=\theta r\).
SECTORS
The area of a sector created by a central angle θ is a fraction of the area of a circle: area of sector = \(\theta \frac{A}{2\pi}\). The equation for area can be substituted in, then the whole equation can be simplified to: area of sector = \(\theta \frac{\pi r^{2}}{2\pi}=\theta \frac{r^{2}}{2}\).
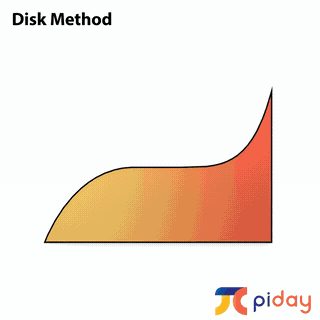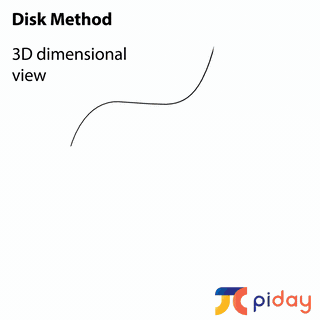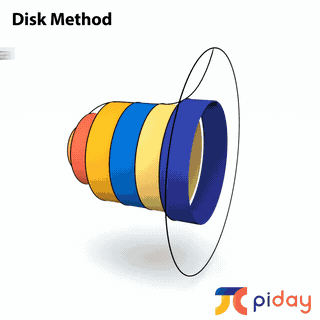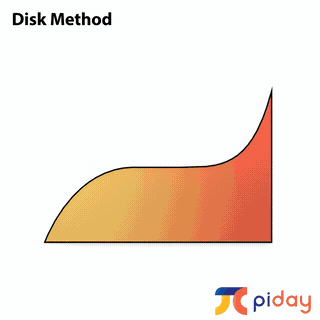
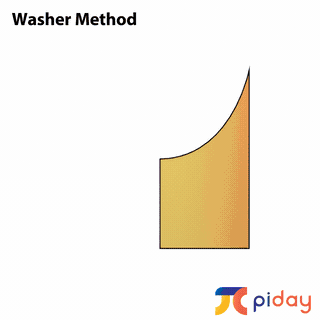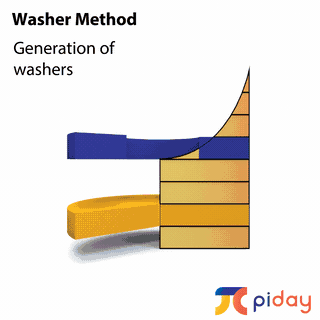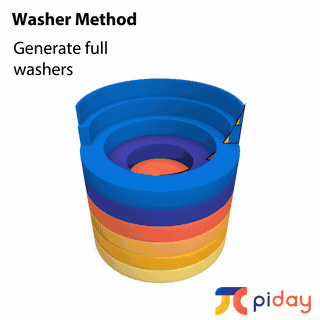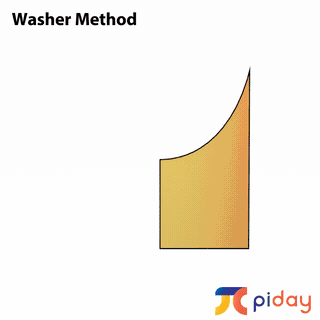
CALCULATING VOLUMES of SOLIDS
In calculus, students learn methods to calculate the volume of solids formed by rotating 2-dimensional surfaces around different axes.
![]()
![]()
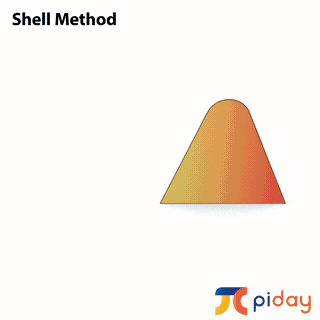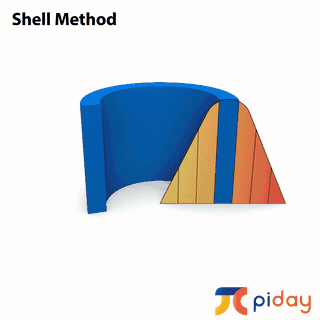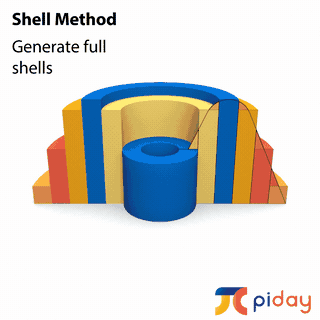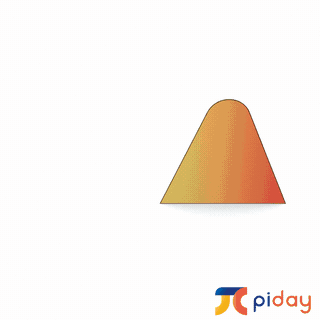
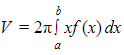
These just scratch the surface! Pi exists in many mathematical and scientific applications. Technological advancements over the last 60 years or so will allow us to explore the famous number even more deeply than ever before! If you’re interested in learning more about pi, there’s no better time to see what’s out there. Have fun!

