How To Find The GCF And LCM
In this article, you will learn how to calculate the Greatest Common Factor (GCF) and Least Common Multiple (LCM) of integers. These skills are helpful in a variety of different situations. Let’s see what they are all about!
Suppose your mom has two rectangular cakes for a party, one vanilla and one strawberry, both the same thickness. The vanilla flavored cake has an area of 12 square inches, while the strawberry flavored cake has an area of 20 square inches. Your mom wants to divide both cakes into pieces such that all pieces are of equal size and both cakes are evenly divided with no leftover smaller pieces.
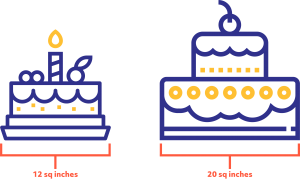
“No problem,” your mom says, “I’ll just cut the cakes into 4-square-inch pieces. That way, everyone will have a same-sized piece.”
How in the world did she know that?
The Greatest Common Factor
Before we explore the cake situation, let’s remember what factors are. Factors are numbers that, when multiplied, produce another number. Usually, we talk about factors in pairs. 1 and 8 are factors of 8 because 1×8=8. The numbers 4 and 2 are also factors of 8, because 4×2=8.
Numbers have a unique prime factorization. Recall that prime numbers, like 2, 3, and 5, can only be divided by themselves and 1. We can keep dividing the factors of any number into its prime number components. So, any number is composed of a unique set of prime numbers multiplied together. Take a look at these factor trees and what they tell us:
Factorizations of 18
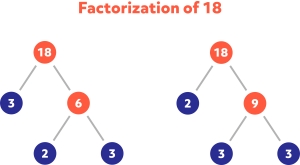
The number 18 is initially factored two different ways: 3 and 6 and also 2 and 9. We can see the prime factorization is the same, regardless of our first factor pair.
2 x 3 x 3 = 18. The purple circles match in both trees.
What does this have to do with the two cakes?
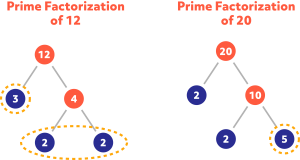
Mathematically, your mom calculated the Greatest Common Factor (GCF) between 12 and 20 to be 4. In other words, 4 is the largest factor that both numbers have in common. We can see it by looking at the prime factorizations of both numbers:
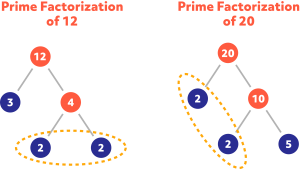
The blue numbers are the prime factors of both numbers. To find the GCF, simply identify the prime factors that both numbers have in common and multiply them together.

Both numbers have common prime factors of 2 and 2. 2 x 2 = 4. This explains how your mom knew to cut both cakes into 4-square-inch pieces!
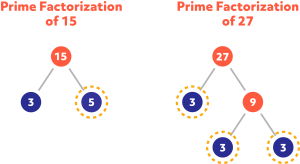
What is the GCF of 15 and 27?
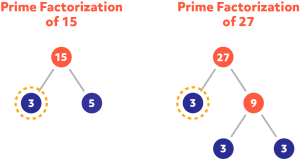
In this case, both numbers only have one common factor, 3. The solution is typically written GCF (15,27) = 3.
What is the GCF of 18 and 36?
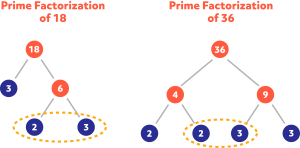
GCF (18,36) = 2 x 3 = 6.
Find the GCF of 7 and 56.
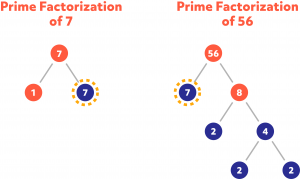
In this case, one of the numbers is prime and it is a factor of the other number. GCF (7,56) = 7.
Find the GCF of 7 and 13.
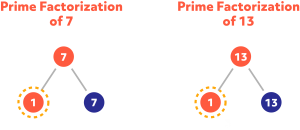
The number 1 is not a prime number, but it is the GCF of 7 and 13, which are both prime numbers.
GCF (7,13) = 1
Let’s briefly return to the cakes. Your mom found that:

and that the GCF is 4, so she should divide the cakes into 4-square-inch pieces. Look at the numbers that are not part of the GCF:

The yellow numbers tell us that there are 3 4-square-inch pieces in the small cake and 5 4-square-inch pieces in the large cake. A total of 8 4-square inch pieces makes sense, because 8×4=32, which equals the cake sizes of 12 and 20 square inches, since 12+20=32.
Suppose 60 girls and 48 boys want to play in a kickball tournament. What is the greatest number of teams that can be formed that have the same ratio of girls to boys? How many girls and boys would each team have?
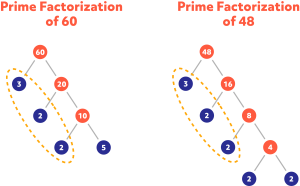
3 x 2 x 2 = 12 teams could be formed, each containing 5 girls and 2 x 2 = 4 boys.
The Least Common Multiple
You’re craving hot dogs, so you head to the store and pick up a pack of dogs and a pack of buns. Typically, a package of franks contains 10, while a pack of buns contains 8. This brings us to one of the great mathematical quandaries of our time. After you eat 8 dogs, you’ll have 2 left, but you’ll be out of buns. You’ll need another pack of buns so the dogs don’t go to waste. Of course, after you eat those, you’ll have 6 buns and no dogs. Off to the store you’ll go, once again, and the cycle continues.

In order to figure out the hot dog problem, we need to find the Least Common Multiple (LCM) of buns and dogs. We need the lowest number that is divisible by both the number of dogs in a pack and buns in a pack. Once we find that number, we can figure out how many packs of each to buy so we don’t have any leftovers.
Let’s start by listing out some multiples of dogs and buns:

There are many common multiples of dogs and buns, but you can see that the LCM of hot dogs and buns is 40. Other common multiples are 80, 120, etc. Buying 4 packs of hot dogs and 5 packs of buns will ensure a dog for every bun. Hope you’re hungry!
Prime factorization can be used here as well. Finding the LCM this way is sort of the opposite as when finding the GCF. For GCF, we want the common factors. For LCM, we want the unique factors. If a factor occurs in both numbers, we want the highest power of that factor. Here goes!
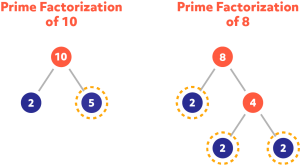
To calculate the LCM, we first need the 5 from factoring 10. Notice that 2 occurs as a factor of both 10 and 8. Remember, we need the highest power of 2:
- The prime factorization of 10 is \(2\times 5 = 2^{1}\times 5\).
- The prime factorization of 8 is \(2\times 2\times 2 = 2^{3}\).
The second number for our calculation is \(2^{3}\), since 3 is higher than \(1.5\times 2^{3}=5\times 8 = 40\), just as we found previously.
LCM (10,8) = 40
What is the LCM of 15 and 27?
LCM (15,27) = \(5\times 3^{3} = 5\times 27 = 135\).
What is the LCM of 18 and 36?
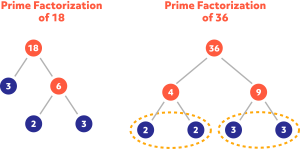
The factorizations of both numbers contain 2 and 3 and the highest power of both of them is 2.
LCM (18,36) = \(2^{2}\times 3^{2} = 4\times 9 = 36\). Notice that 36 is a multiple of 18, also the LCM.
Find the LCM of 7 and 56.
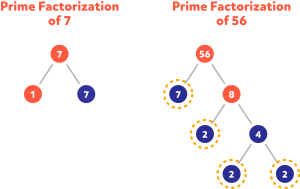
Again, notice one of the numbers is prime and it is a factor of the other number. LCM (7,56) = \(7\times 2^{3}=7\times 8 = 56\).
Find the LCM of 7 and 13.
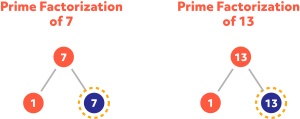
The LCM of 7 and 13, both prime numbers, is simply LCM(7,13) = 7 x 13 = 91.
Starting at 8:00 a.m., a northbound train stops at a station every 12 minutes and a southbound train stops at the same station every 20 minutes. When is the next time both trains will be stopped at the station at the same time?
LCM (12, 20) = \(2^{2}\times 3\times 5= 4\times 3\times 5 = 60\). After 60 min, or at 9:00, is the next time both trains will be at the station at the same time.
There is an east-west train that stops at the station every 8 minutes. When is the next time all 3 trains will be stopped at the station at the same time?
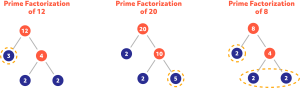
LCM (12,20,8) = \(3\times 5\times 2^{3} = 120\). After 120 minutes, or at 10:00, is the next time all three trains will be at the station at the same time.
Final Thoughts!
When experimenting with factors and multiples, the GCF and LCM often prove useful. Their skills can come in handy for calculations, such as simplifying fractions. However, as we’ve seen, these extend our understanding of multiplication and division, pushing us to truly grasp what it means for a number to be a factor or a multiple, and allow us to make sense of authentic situations. The best part is, all you need to do to practice is pick some numbers. We mostly practiced with two at a time, but you can find the GCF and LCM of any group of numbers. Give it a shot!