Area of a Trapezoid Calculator
How to Calculate the Area of a Trapezoid
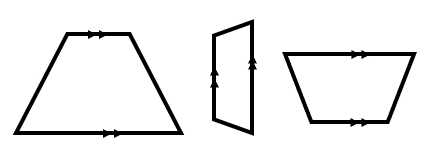
A trapezoid is an interesting four-sided geometric figure. It has two parallel sides and the remaining two sides can be of any length, at any angle. Some possible trapezoid shapes are shown below to clarify the concept. Notice that the parallel lines are marked with arrows.
In real life there are a lot of objects with trapezoid shapes that you may or may not have noticed. See some examples below. Are you surprised?

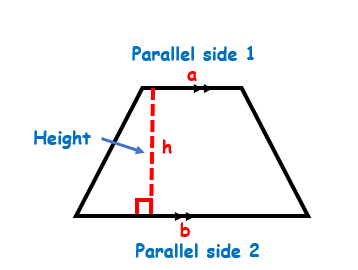
Now that you are clear about the shape of a trapezoid, let’s discuss the parameters you need to know, in order to find its area. There are three important lengths that you need to know to find the area of a trapezoid: lengths of the two parallel sides ‘a’ and ‘b’ and the height. The height is the perpendicular distance between the two parallel sides. By perpendicular distance, we mean that the length of the line that joins parallel side ‘a’ and ‘b’ and is exactly 90 degrees to them.
The area of a trapezoid, A, is given as:
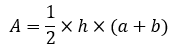
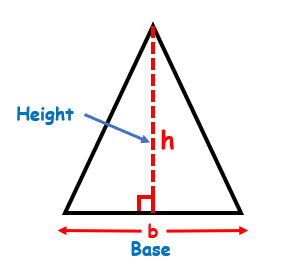
This formula is derived from the concept of the area of a triangle. You might already know how to calculate the area of a triangle, but we will review it briefly, just in case you have forgotten or you don’t know. Two parameters that you need to know to find the area of triangle are the height of the triangle and the base of the triangle. The height of the triangle is given as the perpendicular distance from one corner of the triangle to the base level. Whichever side of the triangle you select as ‘base’, measure the height by considering the corner exactly opposite to the base. See the diagrams below for more clarity on the height-base concept.
Do not get confused if the shape of the triangle is not what you typically expect. Remember the concept of base and height and label accordingly.
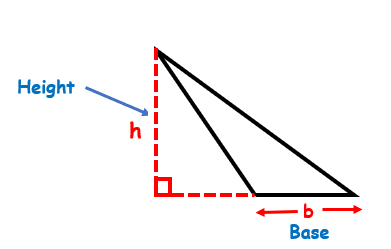
The area of the triangle is given as:
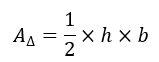
Now, how does this knowledge help us in figuring out the formula of the area of a trapezoid? Let’s see.
Look carefully and you will notice that a trapezoid can be cut diagonally to form two triangles:
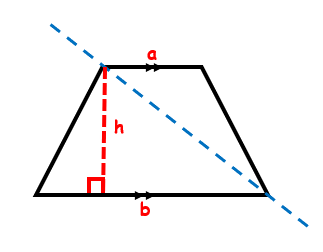
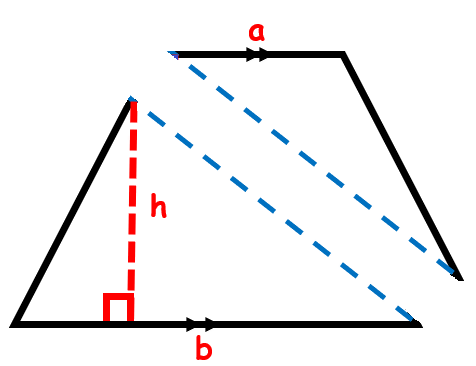
If we find the area of these two triangles and then add them, we will get the area of the whole trapezoid! The base of the upper triangle is length ‘a’ and the base of the lower triangle is the length ‘b’. The height of both triangles is the same.
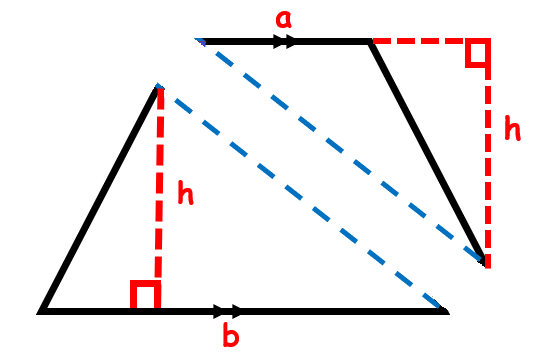
Area of the upper triangle is given as:
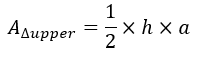
Area of the lower triangle is given as:
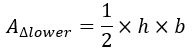
Therefore, area of the trapezoid will be:
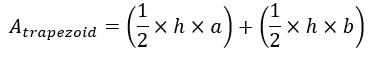
Taking \(\frac{h}{2}\) as the common factor we get:
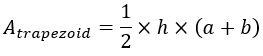
Hopefully, now you fully understand the concept behind the formula of the area of a trapezoid. Let’s do some examples.
Example 1:
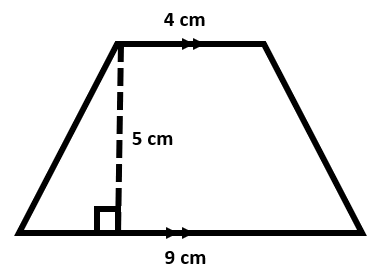
Find the area of the trapezoid given below:
Solution:
From the figure we can see that:
a = 4 cm
b = 9 cm
h = 5 cm
Let area of trapezoid be represented by variable ‘A’
A = ?
Apply the formula for area of a trapezoid:
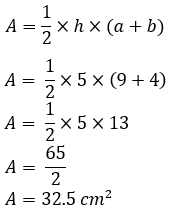
Example 2:
A trapezoid having an area of 98 cm2, has two parallel sides of lengths 16 cm and 12 cm. What is the perpendicular distance between the two parallel sides?
Solution:
We are given the following parameters:
Parallel side 1 = a= 16 cm
Parallel side 2 = b= 12 cm
Area of Trapezoid = A = 98 cm2
We have to find the perpendicular distance between two parallel sides. As we mentioned earlier in the article, it is the height of the trapezoid.
h = ?
Recall the formula for the area of a trapezoid and solve for “h”.
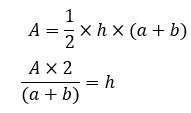
Now, we put in the known values and find the height:
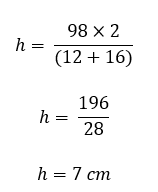
Example 3:
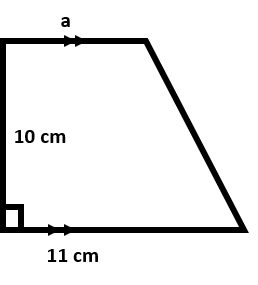
The area of the trapezoid given below is 100 cm2. Find the unknown length of parallel side ‘a’.
Solution:
One side of this trapezium makes a 90-degree angle with both parallel sides. This means that the height of trapezoid and the length of this side is the same. We are there given the following information:
Area of trapezoid = A = 100 cm2
Height = h = 10 cm
Parallel side 2 = b = 11 cm
Parallel side 1 = a = ?
To find ‘a’ we rearrange the formula for area of a trapezoid to solve for “a”:
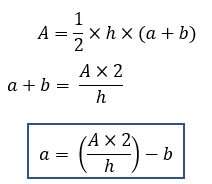
Now, put in the known values to get the final answer:
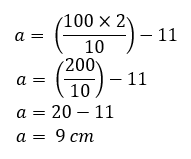
Final Thoughts!
We have tried to cover pretty much everything there is to know about the area of a trapezoid, from its derivation to solving different problems. Geometry is a very important branch of mathematics and learning about all the shapes that exist in the real world is crucial, especially if you are thinking of becoming an engineer one day! After learning the theory, you can use our area of a trapezoid calculator to quickly get answers to your problems and save time!


