Pythagorean Theorem Calculator
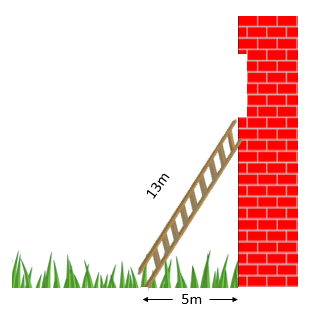
Before we dive into all the formulas and theory, lets imagine a real-life scenario to better understand the importance of learning about the right-angled triangle. Imagine that you want to clean the window of a 1st floor bedroom and you have a 13-meter-long ladder. To reach the window, you place the ladder such that the foot of the ladder is 5 meters away from the wall. Can you tell the height of the window from the ground?
You can if you know the Pythagorean Theorem. Three sides of a right-angled triangle have a unique mathematical relation that was first proven by the Greek mathematician Pythagoras and thats what we are going to learn here. Three sides of a right- angled triangle have special names as shown in the diagram below:
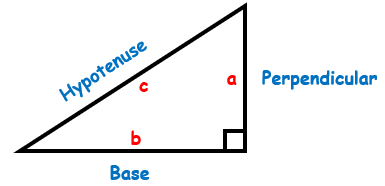
The two sides that form a right angle (90 degrees) to each other are called the ‘perpendicular’ (or ‘height’) and the ‘base’. The side opposite to the right angle is called the ‘hypotenuse’. The Pythagorean Theorem (or sometimes called the Pythagoras Theorem) states that:
The square of the Hypotenuse of a right-angled triangle is equal to the sum of squares of the perpendicular and the base
Mathematically this means:
![]()
This is quite a useful equation and if we know two sides of a right-angled triangle, we can easily calculate the length of the third side.
If we know the base and the perpendicular, the hypotenuse is equal to:
![]()
If the hypotenuse and the base are known, then the perpendicular is equal to:
![]()
Finally, if the hypotenuse and the perpendicular are known then the base is equal to:
![]()

Now, going back to our example:
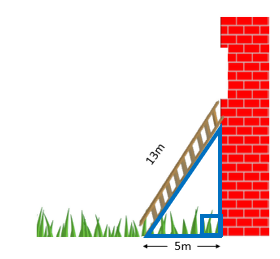
Notice that the ladder against the wall makes a right-angled triangle as the wall is standing up straight (i.e. at exactly 90 degrees to the ground). It is clear now that c = 13 m and b= 5 m and ‘a’ is the unknown that we want to calculate (the height of the window). Knowing the Pythagorean theorem, it is pretty easy now:
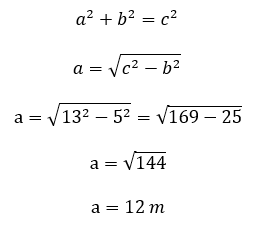
So, the height of the window is 12 meters! Similarly, using the formulas given above, any unknown side of a right-angled triangle can be calculated if the other two sides are given.
You might be wondering how to decide which side is the perpendicular and which one is the base. After all, there are two sides that intersect to make the right angle and the triangle can be in any orientation.
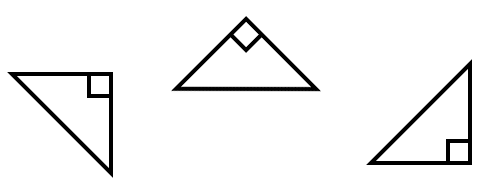
Honestly, it does not matter in case of The Pythagorean Theorem. You just have to be careful about labeling the ‘hypotenuse’, which is always opposite to the right angle. The ‘a’ and ‘b’ sides don’t matter, just label one side of the right angle as ‘a’ and the other as ‘b’.
But the side labeling is important when we use trigonometric functions in relation to the sides of the right-angled triangle. What are simple trigonometric functions? They are the famous: sine (sin), cosine (cos) and tangent (tan). An interesting thing about the right-angled triangle is that if we know one angle other than the right angle (90 degree) and length of one side, we can calculate the length of the other two sides. Let’s see how:
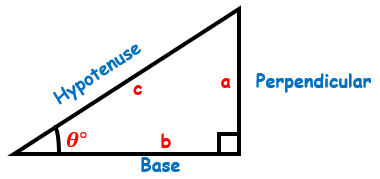
When you know one angle other than the right angle, θo, the side labeling follows these rules:
- Side opposite to the right angle is the hypotenuse
- Side opposite to the angle (θ) is the perpendicular (height)
- The side that makes the angle θ with the hypotenuse is the base
It is important that you remember these rules and label the sides correctly, because the formulas we are going to discuss next are only valid if the sides are labeled as per the rules.
The relation between the sides and the angles is as follows:
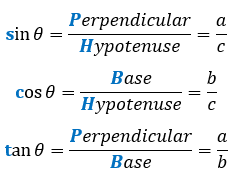
Too difficult to memorize? Don’t worry, there is a short cut to remember these ratios. Just memorize this sentence:
![]()
Notice the capital Blue Letters in the formulas and the sentence and you will get what I am talking about!
Let’s do an example. A right-angled triangle is given below:
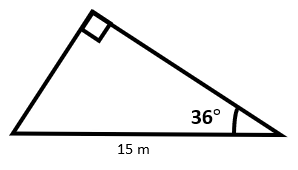
Find the length of the other two sides.
The first step is to label the sides according to the rules.
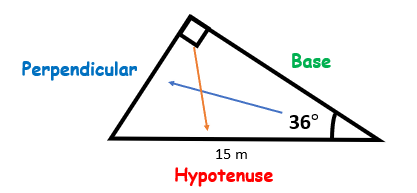
The side opposite the right angle is the hypotenuse, the side opposite the other given angle is the perpendicular and the remaining side is the base.
Now you can easily calculate the length of the perpendicular and base using the above given formulas. Let’s calculate the perpendicular first.

Next, we calculate the base:
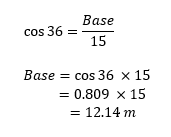
We can verify our answer by checking if the lengths we calculated satisfy the Pythagorean Theorem:
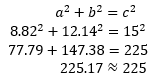
The theorem is verified! This means that all our calculations are correct. Slight error is due to the rounding off in the calculations. If we calculate directly on the calculator, without rounding off any answer, the sum of squares of base and perpendicular will be exactly 225.
Final Thoughts!
So, we learned all about the special properties of a right-angled triangle. These formulas are very important and have a lot of application in real life and various engineering problems. Once you have learned all the important concepts, you can skip hectic calculations and simply use our Pythagorean Calculator to make your life easier! Do explore our website further to learn other topics related to mathematics in an easy and fun way!

