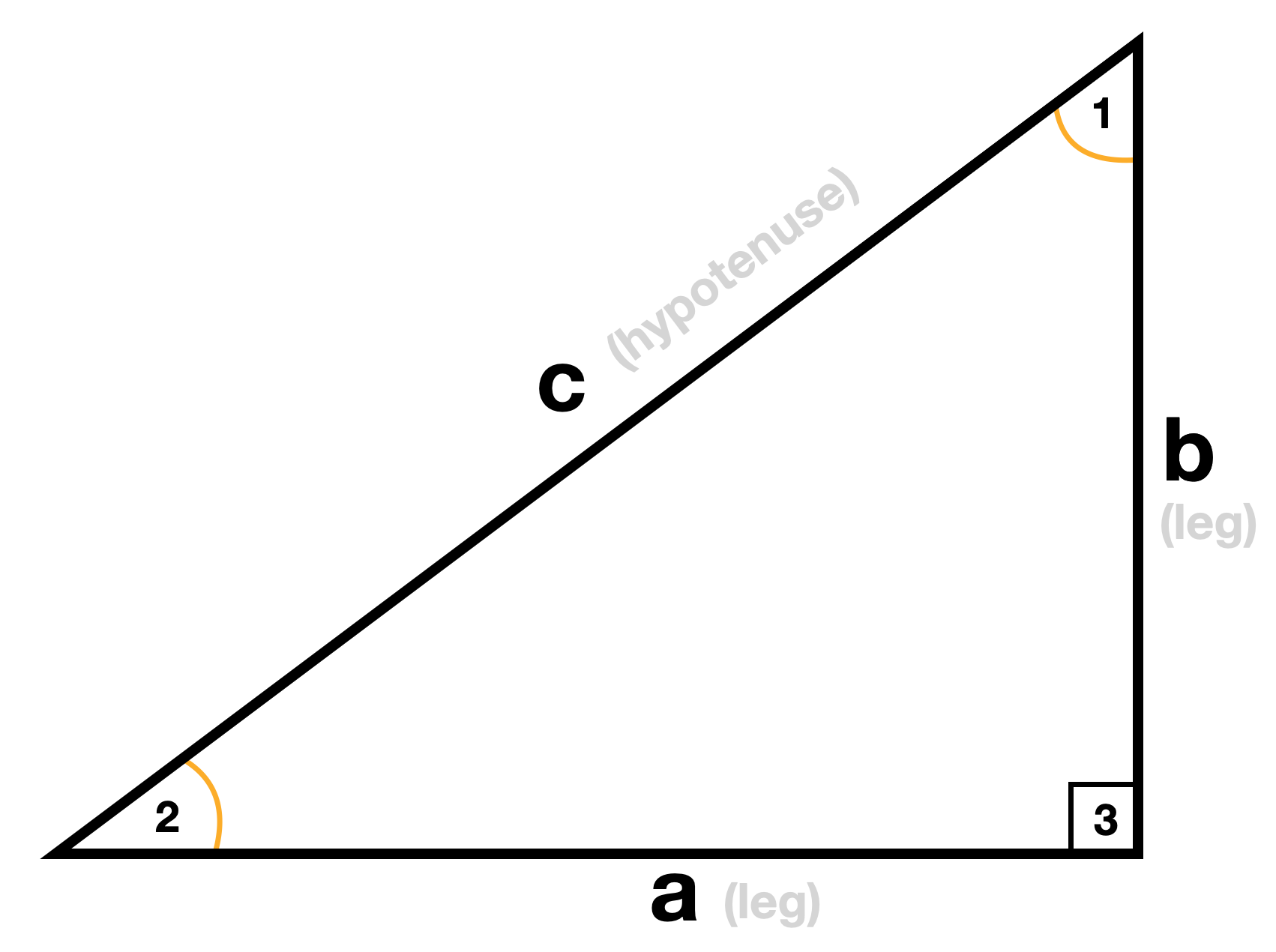
Right Triangle Calculator
To use the right angle calculator simply enter the lengths of any two sides of a right triangle into the top boxes. The calculator will then determine the length of the remaining side, the area and perimeter of the triangle, and all the angles of the triangle.
How to Find the Area and Sides of a Right Triangle
Do it yourself
If we know just two sides of a right triangle, we can use that information to find the third side, the area and perimeter of the triangle, and all the angles of the triangle. Amazing, right? Let’s review how we would find each of those parts.
How to find the Missing Side of a Right Triangle
To find the missing side of a right triangle we use the famous Pythagorean Theorem.
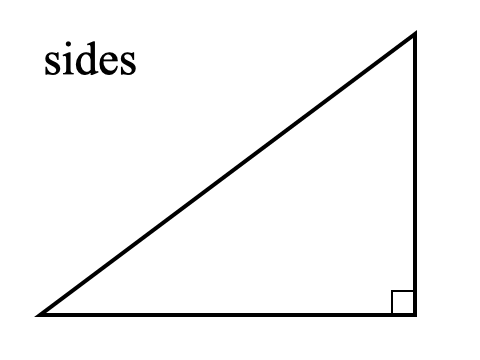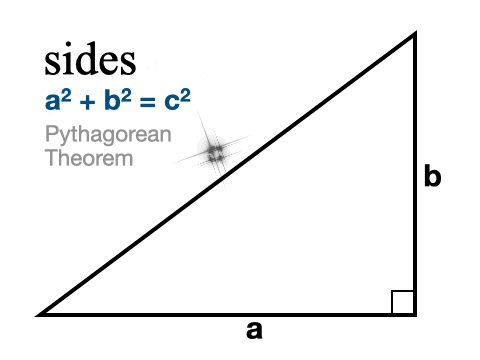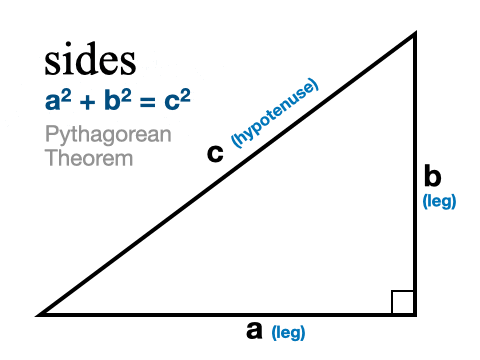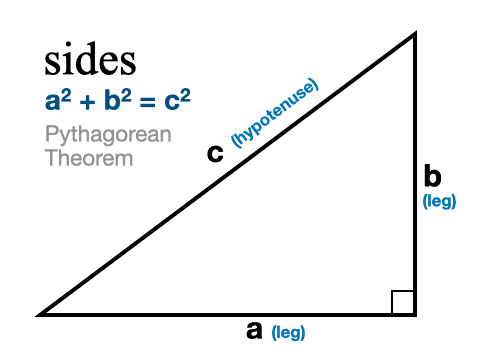
We need to be a little careful that we know which side we’re finding. Right triangles have two legs and a hypotenuse, which is the longest side and is always across from the right angle. When we’re trying to find the hypotenuse we substitute our two known sides for a and b. It doesn’t matter which leg is a and which is b. Then we solve for c by adding the squared values of a and b and taking the square root of both sides.
When we’re trying to find one of the legs we enter the known leg for a and the known hypotenuse for c. Then we solve for b using simple algebra (subtract the value of a squared from both sides, then take the square root of both sides).
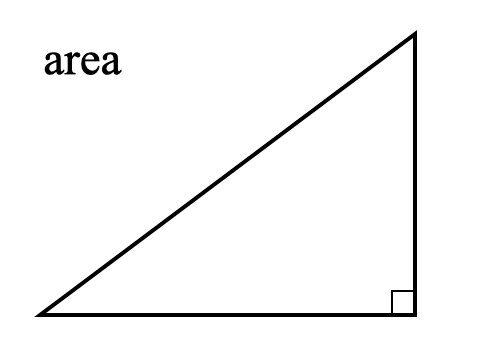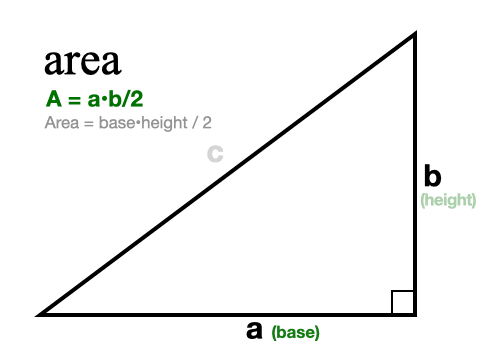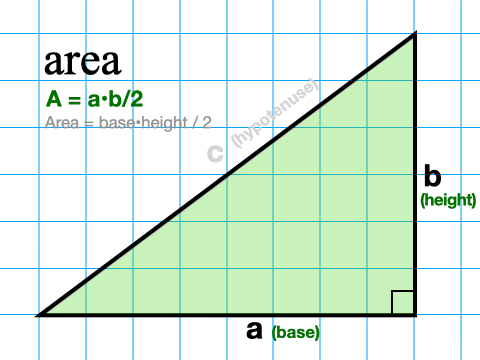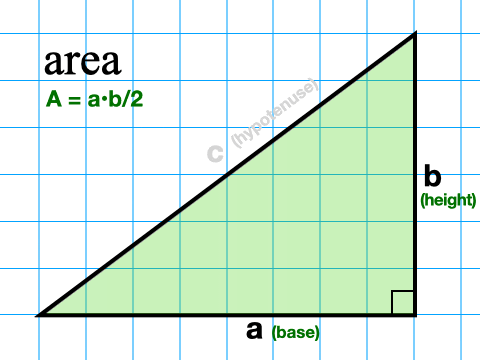
How to find the Area of a Right Triangle
To find the area of a right triangle we only need to know the length of the two legs. We don’t need the hypotenuse at all. That’s because the legs determine the base and the height of the triangle in every right triangle. So we use the general triangle area formula (A = base • height/2) and substitute a and b for base and height. So our new formula for right triangle area is A = ab/2.
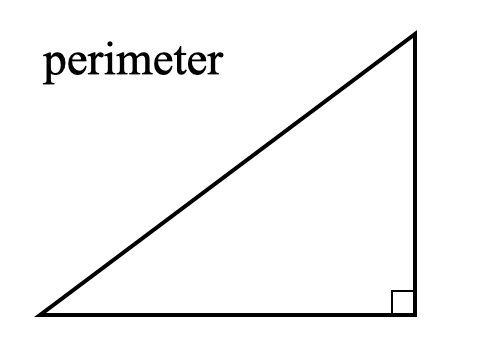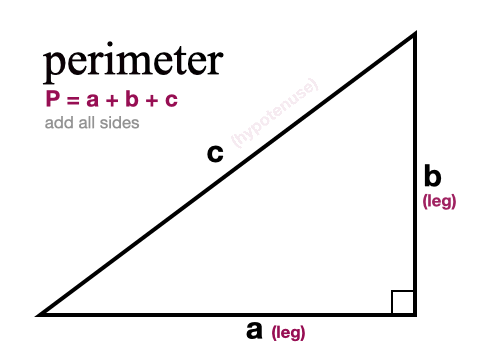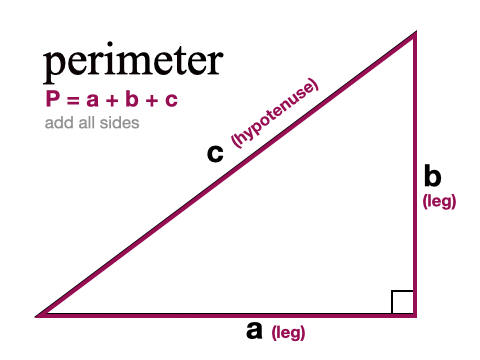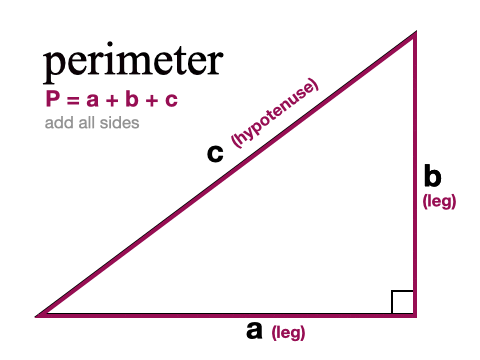
How to find the Perimeter of a Right Triangle
To find the perimeter, or distance around, our triangle we simply need to add all three sides together. If we only know two of the sides we need to use the Pythagorean Theorem first to find the third side.
How to find the Angles of a Right Triangle
To find the angles of a right triangle we use trigonometry. It’s not as difficult as it sounds. We just need to find one special button on our handheld calculators. To start we’ll need to know all the side lengths, so if we don’t know them already we’ll use the Pythagorean Theorem to find them first.
Once we have all the sides we determine which angle we’re going to find. Then we take the side opposite that angle and divide it by the length of the hypotenuse, which is side c. That will give us a value between 0 and 1. Now we just need to find the ARCSIN button on our calculator, which is often labeled as SIN-1. Finding the ARCSIN of our decimal value gives us our angle. Be sure that the calculator is set for angle mode rather than radian mode.
We can repeat this process to find the other unknown angle in the triangle by once again dividing its opposite side by the hypotenuse and then taking the ARCSIN.
Or we could show off even more triangle knowledge by using subtraction to find it since we know the interior angles of a triangle have to add up to 180°. Subtracting the angle we just found from 180° and then subtracting our known right angle (90°) will give us the third angle too.
This calculator is great for getting all this information from just two sides of a right triangle, but it’s a fun challenge to try to find the sides, angles, area and perimeter on our own without it. Then you can use it to check our answers.