Area of a Rectangle Calculator
Jump to Area of a Rectangle
Jump to Calculating the Area of a Rectangle
Jump to Perimeter of a Rectangle
Jump to Calculating the Perimeter of a Rectangle
Jump to Diagonal of a Rectangle
Jump to Calculating the Diagonal of a Rectangle
Jump to Real-life Applications of these Calculations
Go back to Calculators page
How to Calculate the Area of a Rectangle
If you need to find the area and perimeter of a rectangle, this calculator is the handy tool you will need.
By simply inputting the length and width, this calculator will almost instantly find the perimeter (P) and the area (A).
If interested in calculators for a variety of other shapes, you can look at more of our handy calculators. But you can stick around here and learn more about finding the area of a rectangle.
A rectangle has four 90 degree angles. If the lengths of the sides are all the same, then the rectangle is also a square. The lengths of the sides will be given as a or b or you can use l and w for “length” and “width”. The diagonal, which goes from one vertex to the opposite vertex cutting the rectangle into two squares, is called the diagonal and noted as d.
Here are the basic formulas used by the calculator.
Area(A) = a(b)
Perimeter (distance around the outside of the rectangle) = a + a + b + b or 2a + 2b and is noted as (P)
Diagonal is d² = a² + b² which is the Pythagorean Theorem (see our Pythagorean Theorem calculator).
Example of calculating the area of a rectangle:
Suppose the length is a = 6 inches and the width is b = 4 inches
A = a*b , so A = 6(4) = 24 inches²
Using the same dimensions, we can calculate the perimeter.
The perimeter is 2a + 2b, so in this example the perimeter
P = 2(6) + 2(4) = 20 inches
To find the diagonal using the same dimensions:
d² = 6² + 4² = 36 + 16 = 52
Take the square root of both sides and the diagonal d is approximately 7.2 inches
These examples illustrate how to calculate the area, perimeter, and diagonal of a rectangle manually, but if you prefer to use the calculator for quicker results or to merely check your work, then feel free to do so. A great feature of the calculator is that you can find either the length or the width if you know the perimeter and the length of one of the sides.
Area, Perimeter, and Diagonal of a Rectangle
This page will show you how to deal with measuring the area of a rectangle. We will cover the following topics:
What is the area, perimeter, and diagonal of a rectangle?
How to calculate the area, perimeter, and diagonal of a rectangle?
Real-life application in calculating the area, perimeter, and diagonal of a rectangle
Area of a Rectangle
Imagine the area of a rectangle as boxes inside a rectangle. The rectangle below has a covered area of 12 “square units”

The space inside a two-dimensional shape is the area or the amount of covered shape.
This diagram displays the width, length, and area of a rectangle:

Calculating the Area of a Rectangle
To find the area of a rectangle you need to multiply the length and the width of a rectangle. We can get the area of a rectangle by following this formula:
A = L * W
A is the area, L is the length, and W is the width.
Example 1
Calculate the area of a rectangle that has a length of 7 centimeters and a width of 5 centimeters.
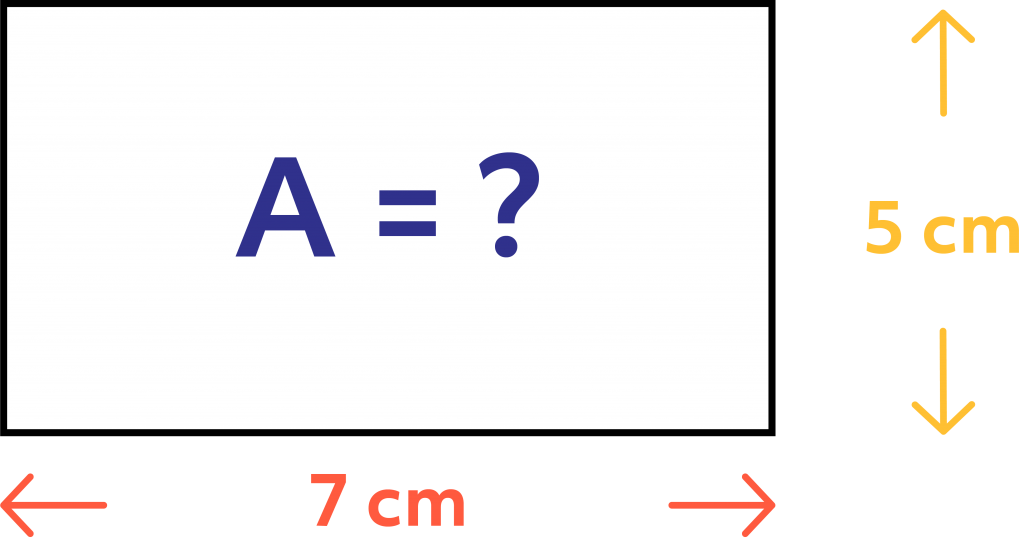
Formula:
A = L * W
Answer:
A = 35. The given length (L) is 7 and 3 is the width (W). When multiplied, you will get 35 as your area.
Perimeter of a Rectangle
Take a look at the image below, a person is walking around the box. The path he walks around from the starting point and back is the perimeter. Knowing the length and width of a rectangle, we can now get the perimeter of a rectangle. Both opposite sides of a rectangle are congruent which means adding those sides, we can calculate for the perimeter.
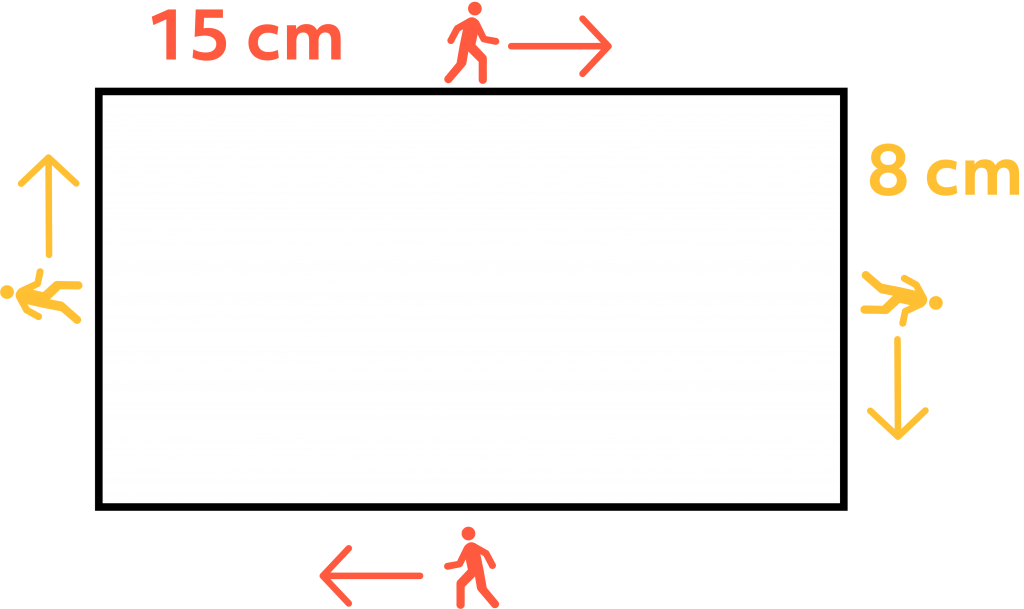
Calculating the Perimeter of a Rectangle
By adding all the sides of a rectangle, we can now get the perimeter. Here’s the equation to get the perimeter of a rectangle:
P = L + W + L + W
Since we know that both opposite sides of a rectangle are identical, we can simplify the equation by using this equation:
P = 2L + 2W
Example 1
Find the perimeter of a rectangle that has a length of 12 centimeters and a width of 7 centimeters.

Formula:
P = L + W + L + W or
P = 2L + 2W
Answer:
P = 12 + 7 + 12 + 7 or
P = 2(12) + 2(7)
The answer is P = 38. By adding 12 (L) + 7 (W) + 12 (L) + 7 (W), you will get 38. By multiplying the Length (L) and Width (W) by 2 then adding the quotients, you will get the same answer.
Diagonal of a Rectangle
If you look closely, a rectangle is a combination of two right angles. A diagonal is the division of a rectangle to form two right triangles identical to one another.

Calculating the Diagonal of a Rectangle
We know that a rectangle is a combination of two right triangles. The diagonal of this rectangle is the hypotenuse of the two triangles which is why we can apply the Pythagorean Theorem to solve for the diagonal of a rectangle. For our formula, use:
\(D = \sqrt{W^{2} + L^{2}}\)
EXAMPLE 1
Solve for the rectangle’s diagonal length whose sides are 15 cm for the length and 8 cm for the width.
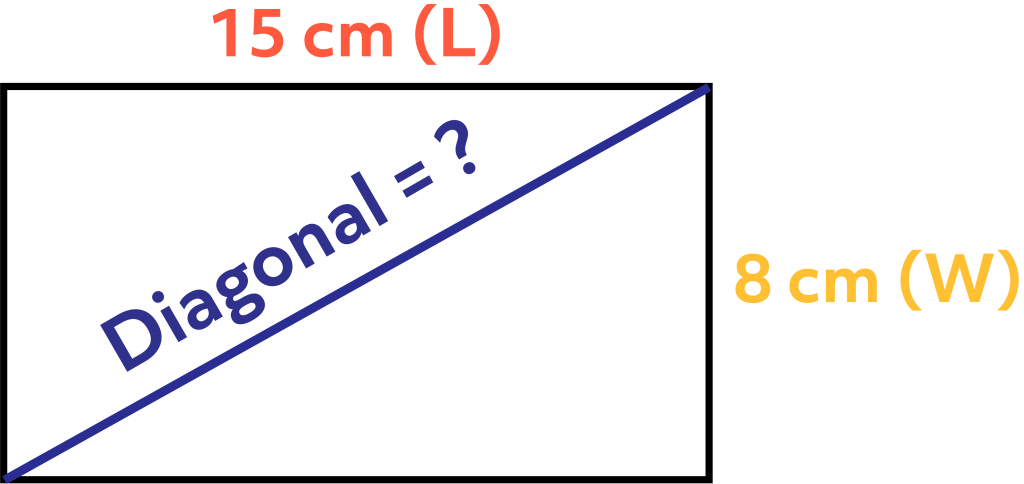
Formula:
\(D = \sqrt{W^{2} + L^{2}}\)
Answer:
\(D = \sqrt{8^{2} + 15^{2}}\) \(D = \sqrt{289}\)
D = 17
The diagonal of the rectangle is 17. Square the values of Width(W) and Length(L), then get the sum of the two squares. Knowing the sum of the two squares, find the square root of the sum.
EXAMPLE 2
Calculate for the diagonal length of a 5 ft long and 3 ft wide rectangle.

Answer:
\(D = \sqrt{3^{2}+5^{2}}\) \(D = \sqrt{34}\)
D = 5.83
Real-life Applications In Getting the Area of a Rectangle
A newly wed couple wants to install tiles to the floor of the master bedroom. The room has a length of 20 ft and a width of 30 ft. The tile they chose has a length of 24 in and 36 in for the width. Solve for the number of tiles needed to fill the master bedroom.
Tips:
1. Solve for the area occupied by the master bedroom.
2. Calculate the area of a tile
3. Choose a unit to be used. This example will use feet.
Solution:
A = L * W
A = 20 ft x 30 ft
A = 600 ft²
Tip:
Before we get the area of each tile, convert the feet to inches
Sample Conversion:
1 foot = 12 inches
2 feet = 24 inches
3 feet = 36 inches
Area of 1 tile = L × W
Area of 1 tile = 2 × 3
Area of 1 tile = 6 ft²
This means that each tile has an area of 6 ft² and it needs to cover the area of the room which is 600 ft². So, 6 × 100 = 600.
The number of tiles needed to fill the master bedroom is 600.
Real-life Applications In Getting the Perimeter of a Rectangle
A farmer wants to add a cage for his chickens. He wants to add a new set of fence near his house and a vacant space with the length of 30 meters and width of 16 meters. Find the perimeter of the vacant space.
Solution:
P = 2L + 2W
Answer:
Perimeter = 2(Length of the vacant space) + 2(Width of the vacant space)
P = 2(30) + 2(16)
P = 60 + 32
P = 92
The Perimeter of the vacant space is 92 meters.
Real-life Applications In Getting the Diagonal of a Rectangle
A sandwich has a length of 12 inches and 8 inches for the width. If you want to equally divide it into two right angles, what would be the length of the diagonal?
Solution:
Equally divide the sandwich into right triangles by using the Pythagorean Theorem:
\(D = \sqrt{W^{2} + L^{2}}\)
Answer:
\(D = \sqrt{8^{2} + 12^{2}}\)\(D = \sqrt{236}\)
D = 14.42
To equally divide the sandwich into two equal right triangles, the length of the diagonal should be 14.42 inches.


